DEMO_Jansen_linkage_animation_01

Below is a demonstration for:

Contents

Keywords

References

clear; close all; clc;

Plot settings

fontSize=25;
lineWidth1=8;
lineWidth2=2;
markerSize=50;

V=[38,7.80000000000000,0;...
   38,22.8000000000000,0;...
   -8.73570000000000,40.5702000000000,0;...
   -39.6678000000000,-5.87170000000000,0;...
   0,0,0;-19.4476000000000,-39.6874000000000,0;...
   17.0047000000000,-35.4306000000000,0;...
   30.3109000000000,-82.5894000000000,0];

E = [1 2; 2 3;3 4;3 5;4 5;4 6;5 7;6 7;6 8;7 8;2 7];
CE = (1:1:size(E,1))';

L=patchEdgeLengths(E,V);

%Determine initial angle of crank
a10=90+atand(abs((V(2,1)-V(1,1))/(V(2,2)-V(1,2))));

VE=patchCentre(E,V);

hf=cFigure; hold on;
he=gedge(E,V,CE,lineWidth1);
pointAnnotate(V,[],'FontSize',fontSize);
pointAnnotate(VE,[],'FontSize',fontSize);

gedge(E,V,'k',1); %Initial
plotV(V,'k.','MarkerSize',15); %Initial

hp=plotV(V,'k.','MarkerSize',markerSize);
axis equal; axis tight; grid on; box on; axis([-80 60 -90 60]);
set(gca,'FontSize',fontSize);
colormap viridis; icolorbar;
%colorbar off; axis off;
drawnow;

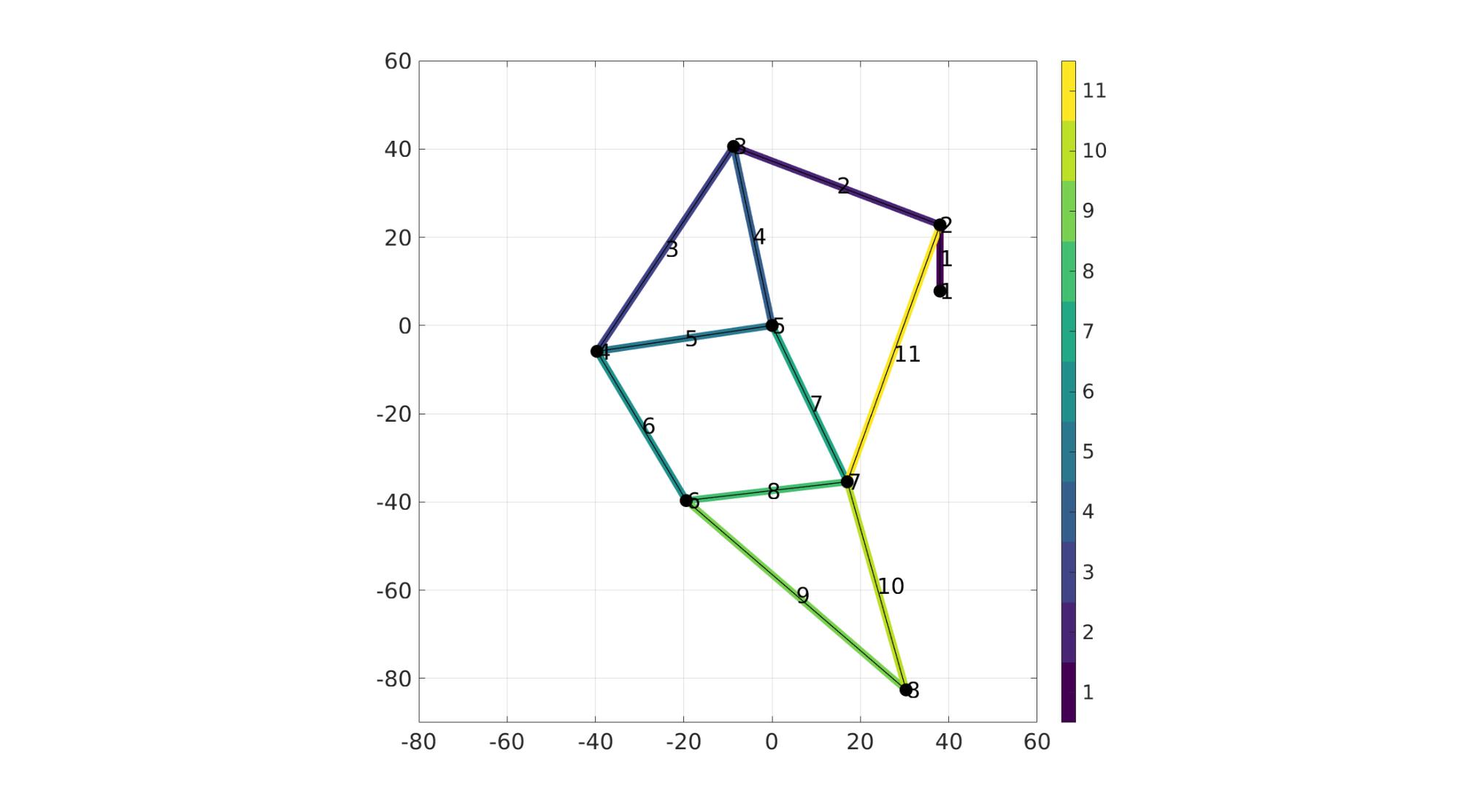
Vt=V;

nSteps=100; %Number of animation steps

%Create angles to set view
aRange=linspace(a10,a10+360,nSteps);

%Create the time vector
animStruct.Time=aRange;

V8t=zeros(nSteps,3);
for q=1:1:nSteps

    a1=aRange(q); %The current angle

    [Vt]=getxyval(a1,E,V);
    V8t(q,:)=Vt(8,:);

    Vt=real(Vt);

    [~,Vtt]=patchDetach(E,Vt);

    %Set entries in animation structure
    animStruct.Handles{q}=[he hp hp hp]; %Handles of objects to animate
    animStruct.Props{q}={'Vertices','XData','YData','ZData'}; %Properties of objects to animate
    animStruct.Set{q}={Vtt,Vt(:,1),Vt(:,2),Vt(:,3)}; %Property values for to set in order to animate
end
plotV(V8t,'r--','LineWidth',lineWidth2);
anim8(hf,animStruct);

function [V]=getxyval(a1,E,V)

g5_34=vecAngle(V(3,:)-V(5,:),V(4,:)-V(5,:));
g7_68=vecAngle(V(6,:)-V(7,:),V(8,:)-V(7,:));


%Compute all lengths
L=patchEdgeLengths(E,V);

%Update coordinate for P2
V(2,1)=cosd(a1)*L(1)+V(1,1);
V(2,2)=sind(a1)*L(1)+V(1,2);

%Distance between P2 and P5
d25=sqrt(sum((V(2,:)-V(5,:)).^2,2));
a25=vecAngle(V(2,:)-V(5,:),[1 0 0]);
g5_23=acosd((L(2)^2-d25^2-L(4)^2)./(-2*d25*L(4)));

%Flip sign of angle when needed
% a4=atand(R41(2)/R41(1));
if dot(V(2,:)-V(5,:),[0 1 0])<0 %&& (a1-a4)<360
    a25=-a25;
end
a3=a25+g5_23;

V(3,1)=cosd(a3)*L(4)+V(5,1);
V(3,2)=sind(a3)*L(4)+V(5,2);

a4=a3+g5_34;

V(4,1)=cosd(a4)*L(5)+V(5,1);
V(4,2)=sind(a4)*L(5)+V(5,2);

g5_27=acosd((L(11)^2-d25^2-L(7)^2)./(-2*d25*L(7)));

a7=-(g5_27-a25);

V(7,1)=cosd(a7)*L(7)+V(5,1);
V(7,2)=sind(a7)*L(7)+V(5,2);

%Distance between P4 and P7
d47=sqrt(sum((V(4,:)-V(7,:)).^2,2));

g7_47_1=acosd((L(5)^2-d47^2-L(7)^2)./(-2*d47*L(7)));
g7_47_2=acosd((L(6)^2-d47^2-L(8)^2)./(-2*d47*L(8)));
g7_47=g7_47_1+g7_47_2;

a57=vecAngle(V(5,:)-V(7,:),[1 0 0]);
a6=g7_47+a57;

V(6,1)=cosd(a6)*L(8)+V(7,1);
V(6,2)=sind(a6)*L(8)+V(7,2);

a10=a6+g7_68;
V(8,1)=cosd(a10)*L(10)+V(7,1);
V(8,2)=sind(a10)*L(10)+V(7,2);

%
% %Create point coordinate array P
% P=[x y];
%
% %Use vector dot product to compute angle between links
% R12=P(2,:)-P(1,:);
% R41=P(1,:)-P(4,:);
% t1=acosd(dot(R12,-R41)./(L1*L4));
%
% %Use law of cosines to compute length of diagonal from P2-P4
% d=sqrt(L1^2+L4^2-2*L1*L4*cosd(t1));
%
% %Use law of cosines to compute angles beta and gamma
% b=acosd((L2^2-L3^2-d^2)/(-2*L3*d));
% g=acosd((L1^2-L4^2-d^2)/(-2*L4*d));
%
% %Flip sign of angle when needed
% a4=atand(R41(2)/R41(1));
% if (a1-a4)>180 && (a1-a4)<360
%     g=-g;
% end
% a3=a4+180-(b+g);
%
% %Update coordinate of P3
% x(3)=cosd(a3)*L3+x(4);
% y(3)=sind(a3)*L3+y(4);

end

function [a]=vecAngle(r1,r2)

a=acosd(dot(r1,r2)./(sqrt(sum(r1.^2))*sqrt(sum(r2.^2))));

end

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2006-2022 Kevin Mattheus Moerman and the GIBBON contributors

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2022b