DEMO_febio_0042_inverse_FEA_cube_uniaxial

Below is a demonstration for:

Inverse FEA based material parameter optimisation for uniaxial compression

Keywords
Control parameters
SIMULATE EXPERIMENTAL DATA
CREATING MESHED BOX
DEFINE BC's
Defining the FEBio input structure
Quick viewing of the FEBio input file structure
Exporting the FEBio input file
Running the FEBio analysis
Import FEBio results
Create structures for optimization
start optimization
Unnormalize and constrain parameters
Unnormalize and constrain parameters
Setting material parameters
START FEBio

Keywords

febio_spec version 4.0
febio, FEBio
hexahedral elements, hex8
static, solid
hyperelastic, Ogden
displacement logfile
stress logfile

clear; close all; clc;

Plot settings

fontSize=20;
faceAlpha1=0.8;
faceAlpha2=1;
edgeColor=0.25*ones(1,3);
edgeWidth=1.5;
markerSize=25;
markerSize2=50;
lineWidth=5;
lineWidth2=3;
cMap=viridis(20);

Control parameters

% Path names
defaultFolder = fileparts(fileparts(mfilename('fullpath')));
savePath=fullfile(defaultFolder,'data','temp');

% Defining file names
febioFebFileNamePart='tempModel';
febioFebFileName=fullfile(savePath,[febioFebFileNamePart,'.feb']); %FEB file name
febioLogFileName=[febioFebFileNamePart,'.txt']; %FEBio log file name
febioLogFileName_disp=[febioFebFileNamePart,'_disp_out.txt']; %Log file name for exporting displacement
febioLogFileName_force=[febioFebFileNamePart,'_force_out.txt']; %Log file name for exporting force
febioLogFileName_stress=[febioFebFileNamePart,'_stress_out.txt']; %Log file name for exporting stress sigma_z
febioLogFileName_stretch=[febioFebFileNamePart,'_stretch_out.txt']; %Log file name for exporting stretch U_z

%Specifying dimensions and number of elements
sampleWidth=10;
sampleThickness=10;
sampleHeight=10;
pointSpacings=10*ones(1,3);
initialArea=sampleWidth*sampleThickness;

numElementsWidth=round(sampleWidth/pointSpacings(1));
numElementsThickness=round(sampleThickness/pointSpacings(2));
numElementsHeight=round(sampleHeight/pointSpacings(3));

stretchLoad=0.7;
displacementMagnitude=(stretchLoad*sampleHeight)-sampleHeight;

%True material parameter set
k_factor=1e2;
c1_true=0.000322322142618;
m1_true=6;
k_true=c1_true*k_factor;

%Initial material parameter set
c1_ini=c1_true*2;
m1_ini=m1_true/2;
k_ini=c1_ini*k_factor;
P=[c1_ini m1_ini];

% FEA control settings
numTimeSteps=10; %Number of time steps desired
max_refs=25; %Max reforms
max_ups=0; %Set to zero to use full-Newton iterations
opt_iter=6; %Optimum number of iterations
max_retries=5; %Maximum number of retires
dtmin=(1/numTimeSteps)/100; %Minimum time step size
dtmax=1/numTimeSteps; %Maximum time step size

runMode='external';% 'internal' or 'external'

SIMULATE EXPERIMENTAL DATA

%Basic set
stress_cauchy_exp=1/1000*[-0.606636933451196;-0.594598753306976;-0.582704841004989;-0.571357405135258;-0.560202987257958;-0.549116632489736;-0.538518403222691;-0.528087294560408;-0.518193056737126;-0.508206114096577;-0.498701595140669;-0.489855637164223;-0.480813541456146;-0.472386398119889;-0.463619435755875;-0.455563887366101;-0.447492483369391;-0.439573886089611;-0.432050298442763;-0.424607647116797;-0.416804189884078;-0.410387298955262;-0.402977977822379;-0.396396657790034;-0.389210485373911;-0.383000553144204;-0.376675743693335;-0.370668858911072;-0.364731155035823;-0.358344772157269;-0.352790185960043;-0.346625957990168;-0.340956058045645;-0.335892515500584;-0.330212348100342;-0.325153422018813;-0.319890421672462;-0.315056500840712;-0.310859570288282;-0.305563240532117;-0.301114864342368;-0.295807178919732;-0.291944875824590;-0.287799721606394;-0.282704271932097;-0.279560319546267;-0.273953092186896;-0.271205596632553;-0.266019580975468;-0.261921529885230;-0.259473236771767;-0.254229845700605;-0.251227010966108;-0.246731599709182;-0.243347463269765;-0.240668206009318;-0.235904450179518;-0.233443491646300;-0.229240342796589;-0.226328455230997;-0.222574693739149;-0.219690552720043;-0.215908110296801;-0.213462994691799;-0.209402262394587;-0.206143135063048;-0.204259473767410;-0.200271046174199;-0.198497342254049;-0.194018107075590;-0.190682588685824;-0.190178278993820;-0.184939186637633;-0.184540226448861;-0.179325520197559;-0.177302998325867;-0.174896317893232;-0.170891038492450;-0.170506389072493;-0.165503062182587;-0.164964944739691;-0.160899776454826;-0.158388071874370;-0.156732253086585;-0.152865980799647;-0.151886036142296;-0.147064551962397;-0.146636586148680;-0.143247545748075;-0.139910407552933;-0.139643630040939;-0.135175245456319;-0.134411814767664;-0.131535143940800;-0.127943005303573;-0.127499404828055;-0.123718865018965;-0.123269655840332;-0.118450118919226;-0.117869603457104;-0.114259063948408;-0.111845005007273;-0.110782903827826;-0.106815200840467;-0.108112322079051;-0.103218831561054;-0.103859461792770;-0.100330051927225;-0.0988503888488038;-0.0984110683795259;-0.0920373613042230;-0.0944900398318279;-0.0908054642234128;-0.0873647791392896;-0.0857302637239363;-0.0832930518728098;-0.0811377337125286;-0.0801419455213994;-0.0773146108678843;-0.0750524119380378;-0.0737660915109812;-0.0711063097725948;-0.0689106003957611;-0.0662015603338655;-0.0637907034798034;-0.0622238776663924;-0.0587129121234732;-0.0590737570248270;-0.0542752113831988;-0.0539468997803651;-0.0504474583208646;-0.0479308792263506;-0.0474997497002284;-0.0422136232687380;-0.0419340474843669;-0.0383206523546593;-0.0353822402853126;-0.0342394575632298;-0.0296092241247699;-0.0290386117855990;-0.0252785740102147;-0.0211393477778685;-0.0210232271972257;-0.0149625128602809;-0.0150455267730763;-0.00925788965002460;-0.00559693887219605;-0.00235368730112040;0.00439939147625970;0.00280776088737496];
stretch_exp=[0.700330019000000;0.702340563275168;0.704351107550336;0.706361651825503;0.708372196100671;0.710382740375839;0.712393284651007;0.714403828926175;0.716414373201342;0.718424917476510;0.720435461751678;0.722446006026846;0.724456550302013;0.726467094577181;0.728477638852349;0.730488183127517;0.732498727402685;0.734509271677852;0.736519815953020;0.738530360228188;0.740540904503356;0.742551448778524;0.744561993053691;0.746572537328859;0.748583081604027;0.750593625879195;0.752604170154362;0.754614714429530;0.756625258704698;0.758635802979866;0.760646347255034;0.762656891530201;0.764667435805369;0.766677980080537;0.768688524355705;0.770699068630873;0.772709612906040;0.774720157181208;0.776730701456376;0.778741245731544;0.780751790006711;0.782762334281879;0.784772878557047;0.786783422832215;0.788793967107383;0.790804511382550;0.792815055657718;0.794825599932886;0.796836144208054;0.798846688483222;0.800857232758389;0.802867777033557;0.804878321308725;0.806888865583893;0.808899409859060;0.810909954134228;0.812920498409396;0.814931042684564;0.816941586959732;0.818952131234899;0.820962675510067;0.822973219785235;0.824983764060403;0.826994308335570;0.829004852610738;0.831015396885906;0.833025941161074;0.835036485436242;0.837047029711409;0.839057573986577;0.841068118261745;0.843078662536913;0.845089206812081;0.847099751087248;0.849110295362416;0.851120839637584;0.853131383912752;0.855141928187920;0.857152472463087;0.859163016738255;0.861173561013423;0.863184105288591;0.865194649563758;0.867205193838926;0.869215738114094;0.871226282389262;0.873236826664430;0.875247370939597;0.877257915214765;0.879268459489933;0.881279003765101;0.883289548040269;0.885300092315436;0.887310636590604;0.889321180865772;0.891331725140940;0.893342269416107;0.895352813691275;0.897363357966443;0.899373902241611;0.901384446516779;0.903394990791946;0.905405535067114;0.907416079342282;0.909426623617450;0.911437167892617;0.913447712167785;0.915458256442953;0.917468800718121;0.919479344993289;0.921489889268456;0.923500433543624;0.925510977818792;0.927521522093960;0.929532066369128;0.931542610644295;0.933553154919463;0.935563699194631;0.937574243469799;0.939584787744967;0.941595332020134;0.943605876295302;0.945616420570470;0.947626964845638;0.949637509120805;0.951648053395973;0.953658597671141;0.955669141946309;0.957679686221477;0.959690230496644;0.961700774771812;0.963711319046980;0.965721863322148;0.967732407597316;0.969742951872483;0.971753496147651;0.973764040422819;0.975774584697987;0.977785128973154;0.979795673248322;0.981806217523490;0.983816761798658;0.985827306073826;0.987837850348993;0.989848394624161;0.991858938899329;0.993869483174497;0.995880027449664;0.997890571724832;0.999901116000000];

%Interpolate to higher sampling
n=100;
stretch_exp_n=linspace(1,stretchLoad,n);
stress_cauchy_exp_n = interp1(stretch_exp,stress_cauchy_exp,stretch_exp_n,'pchip');

%Override variables
stress_cauchy_exp=stress_cauchy_exp_n;
stretch_exp=stretch_exp_n;

%Add noise
stdNoise=0.01; %Standard deviation in units of stress
stress_cauchy_exp_n=stress_cauchy_exp_n+stdNoise.*randn(size(stress_cauchy_exp_n));

CREATING MESHED BOX

%Create box 1
boxDim=[sampleWidth sampleThickness sampleHeight]; %Dimensions
boxEl=[numElementsWidth numElementsThickness numElementsHeight]; %Number of elements
[box1]=hexMeshBox(boxDim,boxEl);
E=box1.E;
V=box1.V;
Fb=box1.Fb;
faceBoundaryMarker=box1.faceBoundaryMarker;

X=V(:,1); Y=V(:,2); Z=V(:,3);
VE=[mean(X(E),2) mean(Y(E),2) mean(Z(E),2)];

elementMaterialIndices=ones(size(E,1),1);

% Plotting boundary surfaces

cFigure; hold on;
title('Model surfaces','FontSize',fontSize);
gpatch(Fb,V,faceBoundaryMarker,'k',0.5);
colormap(gjet(6)); icolorbar;
axisGeom(gca,fontSize);
drawnow;

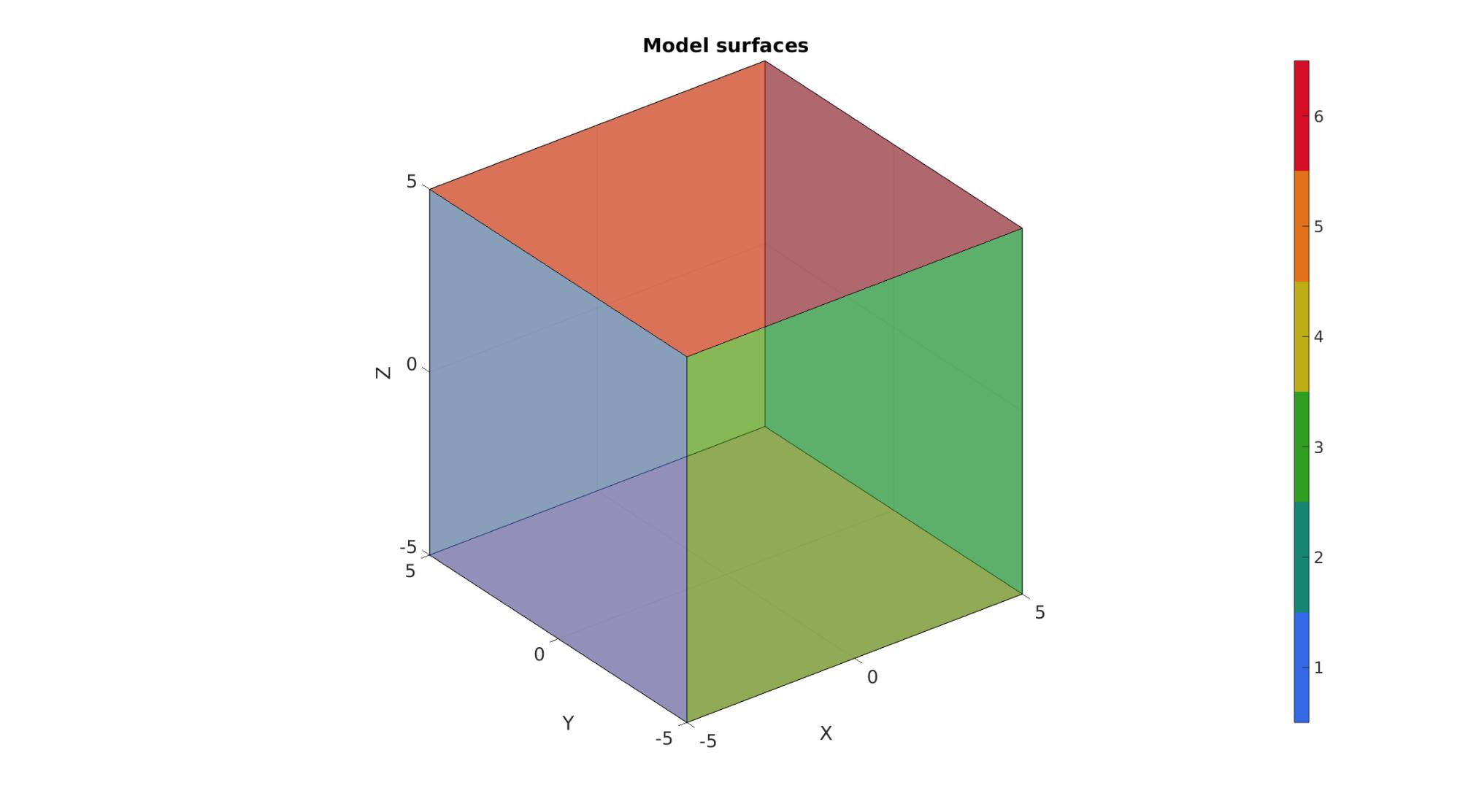
DEFINE BC's

%Define supported node sets
logicFace=faceBoundaryMarker==1;
Fr=Fb(logicFace,:);
bcSupportList_X=unique(Fr(:));

logicFace=faceBoundaryMarker==3;
Fr=Fb(logicFace,:);
bcSupportList_Y=unique(Fr(:));

logicFace=faceBoundaryMarker==5;
Fr=Fb(logicFace,:);
bcSupportList_Z=unique(Fr(:));

%Prescribed displacement nodes
logicPrescribe=faceBoundaryMarker==6;
Fr=Fb(logicPrescribe,:);
bcPrescribeList=unique(Fr(:));

Visualize BC's

cFigure; hold on;
title('Complete model','FontSize',fontSize);

gpatch(Fb,V,'kw','k',0.5);
plotV(V(bcSupportList_X,:),'r.','MarkerSize',markerSize);
plotV(V(bcSupportList_Y,:),'g.','MarkerSize',markerSize);
plotV(V(bcSupportList_Z,:),'b.','MarkerSize',markerSize);
plotV(V(bcPrescribeList,:),'k.','MarkerSize',markerSize);

axisGeom(gca,fontSize);
drawnow;

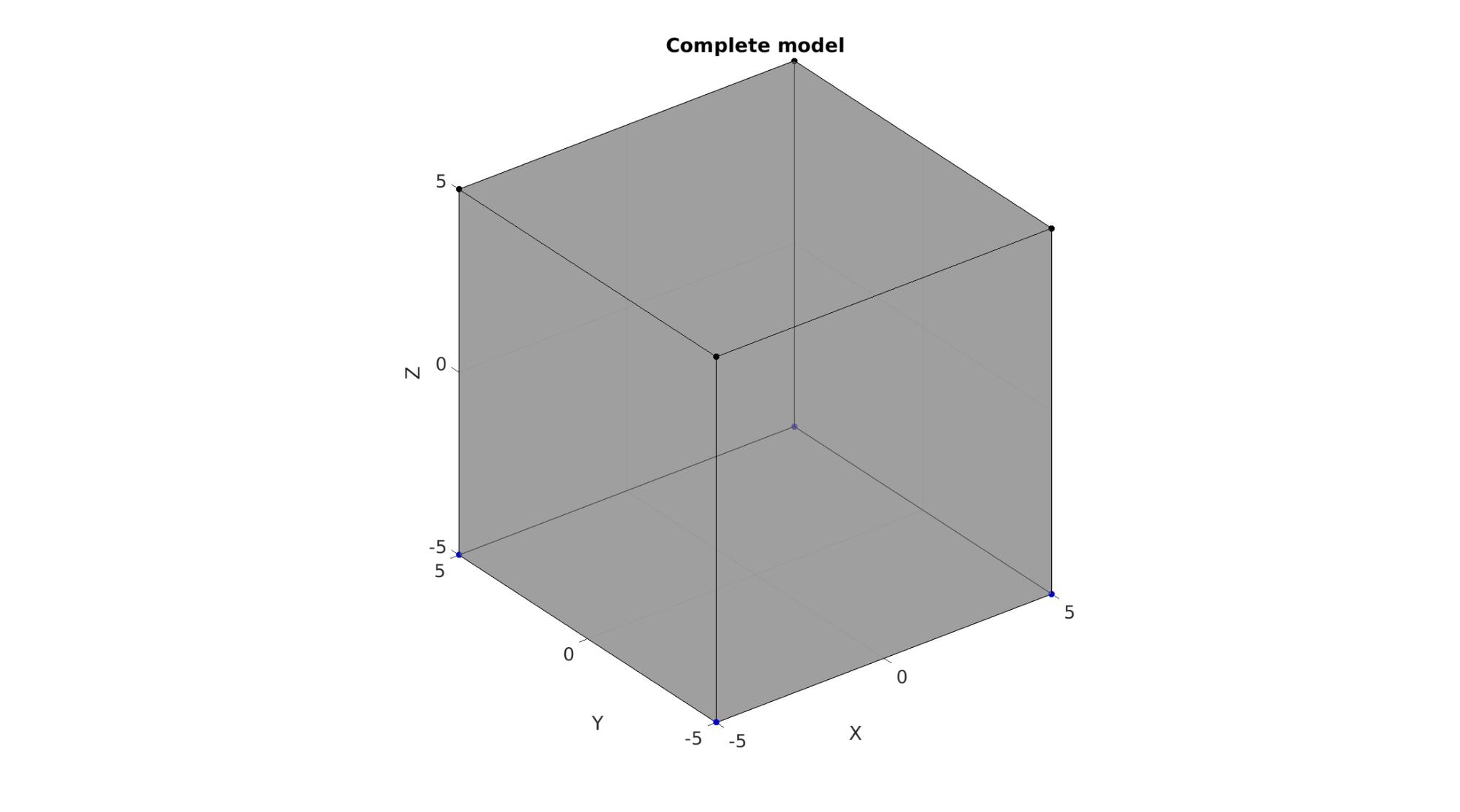
Defining the FEBio input structure

See also febioStructTemplate and febioStruct2xml and the FEBio user manual.

%Get a template with default settings
[febio_spec]=febioStructTemplate;

%febio_spec version
febio_spec.ATTR.version='4.0';

%Module section
febio_spec.Module.ATTR.type='solid';

%Control section
febio_spec.Control.analysis='STATIC';
febio_spec.Control.time_steps=numTimeSteps;
febio_spec.Control.step_size=1/numTimeSteps;
febio_spec.Control.solver.max_refs=max_refs;
febio_spec.Control.solver.qn_method.max_ups=max_ups;
febio_spec.Control.time_stepper.dtmin=dtmin;
febio_spec.Control.time_stepper.dtmax=dtmax;
febio_spec.Control.time_stepper.max_retries=max_retries;
febio_spec.Control.time_stepper.opt_iter=opt_iter;

%Material section
materialName1='Material1';
febio_spec.Material.material{1}.ATTR.name=materialName1;
febio_spec.Material.material{1}.ATTR.type='Ogden';
febio_spec.Material.material{1}.ATTR.id=1;
febio_spec.Material.material{1}.c1=c1_ini;
febio_spec.Material.material{1}.m1=m1_ini;
febio_spec.Material.material{1}.c2=c1_ini;
febio_spec.Material.material{1}.m2=-m1_ini;
febio_spec.Material.material{1}.k=k_ini;

% Mesh section
% -> Nodes
febio_spec.Mesh.Nodes{1}.ATTR.name='Object1'; %The node set name
febio_spec.Mesh.Nodes{1}.node.ATTR.id=(1:size(V,1))'; %The node id's
febio_spec.Mesh.Nodes{1}.node.VAL=V; %The nodel coordinates

% -> Elements
partName1='Part1';
febio_spec.Mesh.Elements{1}.ATTR.name=partName1; %Name of this part
febio_spec.Mesh.Elements{1}.ATTR.type='hex8'; %Element type
febio_spec.Mesh.Elements{1}.elem.ATTR.id=(1:1:size(E,1))'; %Element id's
febio_spec.Mesh.Elements{1}.elem.VAL=E; %The element matrix

% -> NodeSets
nodeSetName1='bcSupportList_X';
nodeSetName2='bcSupportList_Y';
nodeSetName3='bcSupportList_Z';
nodeSetName4='bcPrescribeList';

febio_spec.Mesh.NodeSet{1}.ATTR.name=nodeSetName1;
febio_spec.Mesh.NodeSet{1}.VAL=mrow(bcSupportList_X);

febio_spec.Mesh.NodeSet{2}.ATTR.name=nodeSetName2;
febio_spec.Mesh.NodeSet{2}.VAL=mrow(bcSupportList_Y);

febio_spec.Mesh.NodeSet{3}.ATTR.name=nodeSetName3;
febio_spec.Mesh.NodeSet{3}.VAL=mrow(bcSupportList_Z);

febio_spec.Mesh.NodeSet{4}.ATTR.name=nodeSetName4;
febio_spec.Mesh.NodeSet{4}.VAL=mrow(bcPrescribeList);

%MeshDomains section
febio_spec.MeshDomains.SolidDomain.ATTR.name=partName1;
febio_spec.MeshDomains.SolidDomain.ATTR.mat=materialName1;

%Boundary condition section
% -> Fix boundary conditions
febio_spec.Boundary.bc{1}.ATTR.name='zero_displacement_x';
febio_spec.Boundary.bc{1}.ATTR.type='zero displacement';
febio_spec.Boundary.bc{1}.ATTR.node_set=nodeSetName1;
febio_spec.Boundary.bc{1}.x_dof=1;
febio_spec.Boundary.bc{1}.y_dof=0;
febio_spec.Boundary.bc{1}.z_dof=0;

febio_spec.Boundary.bc{2}.ATTR.name='zero_displacement_y';
febio_spec.Boundary.bc{2}.ATTR.type='zero displacement';
febio_spec.Boundary.bc{2}.ATTR.node_set=nodeSetName2;
febio_spec.Boundary.bc{2}.x_dof=0;
febio_spec.Boundary.bc{2}.y_dof=1;
febio_spec.Boundary.bc{2}.z_dof=0;

febio_spec.Boundary.bc{3}.ATTR.name='zero_displacement_z';
febio_spec.Boundary.bc{3}.ATTR.type='zero displacement';
febio_spec.Boundary.bc{3}.ATTR.node_set=nodeSetName3;
febio_spec.Boundary.bc{3}.x_dof=0;
febio_spec.Boundary.bc{3}.y_dof=0;
febio_spec.Boundary.bc{3}.z_dof=1;

febio_spec.Boundary.bc{4}.ATTR.name='prescibed_displacement_z';
febio_spec.Boundary.bc{4}.ATTR.type='prescribed displacement';
febio_spec.Boundary.bc{4}.ATTR.node_set=nodeSetName4;
febio_spec.Boundary.bc{4}.dof='z';
febio_spec.Boundary.bc{4}.value.ATTR.lc=1;
febio_spec.Boundary.bc{4}.value.VAL=displacementMagnitude;
febio_spec.Boundary.bc{4}.relative=0;

%LoadData section
% -> load_controller
febio_spec.LoadData.load_controller{1}.ATTR.name='LC_1';
febio_spec.LoadData.load_controller{1}.ATTR.id=1;
febio_spec.LoadData.load_controller{1}.ATTR.type='loadcurve';
febio_spec.LoadData.load_controller{1}.interpolate='LINEAR';
%febio_spec.LoadData.load_controller{1}.extend='CONSTANT';
febio_spec.LoadData.load_controller{1}.points.pt.VAL=[0 0; 1 1];

%Output section
% -> log file
febio_spec.Output.logfile.ATTR.file=febioLogFileName;
febio_spec.Output.logfile.node_data{1}.ATTR.file=febioLogFileName_disp;
febio_spec.Output.logfile.node_data{1}.ATTR.data='ux;uy;uz';
febio_spec.Output.logfile.node_data{1}.ATTR.delim=',';

febio_spec.Output.logfile.node_data{2}.ATTR.file=febioLogFileName_force;
febio_spec.Output.logfile.node_data{2}.ATTR.data='Rx;Ry;Rz';
febio_spec.Output.logfile.node_data{2}.ATTR.delim=',';

febio_spec.Output.logfile.element_data{1}.ATTR.file=febioLogFileName_stress;
febio_spec.Output.logfile.element_data{1}.ATTR.data='sz';
febio_spec.Output.logfile.element_data{1}.ATTR.delim=',';

febio_spec.Output.logfile.element_data{2}.ATTR.file=febioLogFileName_stretch;
febio_spec.Output.logfile.element_data{2}.ATTR.data='Uz';
febio_spec.Output.logfile.element_data{2}.ATTR.delim=',';

% Plotfile section
febio_spec.Output.plotfile.compression=0;

Quick viewing of the FEBio input file structure

The febView function can be used to view the xml structure in a MATLAB figure window.

febView(febio_spec); %Viewing the febio file

Exporting the FEBio input file

Exporting the febio_spec structure to an FEBio input file is done using the febioStruct2xml function.

febioStruct2xml(febio_spec,febioFebFileName); %Exporting to file and domNode
%system(['gedit ',febioFebFileName,' &']);

Running the FEBio analysis

To run the analysis defined by the created FEBio input file the runMonitorFEBio function is used. The input for this function is a structure defining job settings e.g. the FEBio input file name. The optional output runFlag informs the user if the analysis was run succesfully.

febioAnalysis.run_filename=febioFebFileName; %The input file name
febioAnalysis.run_logname=febioLogFileName; %The name for the log file
febioAnalysis.disp_on=1; %Display information on the command window
febioAnalysis.runMode=runMode;
febioAnalysis.maxLogCheckTime=10; %Max log file checking time

[runFlag]=runMonitorFEBio(febioAnalysis);%START FEBio NOW!!!!!!!!

 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
-------->    RUNNING/MONITORING FEBIO JOB    <-------- 31-May-2023 15:54:04
FEBio path: /home/kevin/FEBioStudio/bin/febio4
# Attempt removal of existing log files                31-May-2023 15:54:04
 * Removal succesful                                   31-May-2023 15:54:04
# Attempt removal of existing .xplt files              31-May-2023 15:54:04
 * Removal succesful                                   31-May-2023 15:54:04
# Starting FEBio...                                    31-May-2023 15:54:04
  Max. total analysis time is: Inf s
 * Waiting for log file creation                       31-May-2023 15:54:04
   Max. wait time: 10 s
 * Log file found.                                     31-May-2023 15:54:04
# Parsing log file...                                  31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.1                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.2                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.3                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.4                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.5                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.6                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.7                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.8                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 0.9                        31-May-2023 15:54:04
    number of iterations   : 3                         31-May-2023 15:54:04
    number of reformations : 3                         31-May-2023 15:54:04
------- converged at time : 1                          31-May-2023 15:54:04
 Elapsed time : 0:00:00                                31-May-2023 15:54:04
 N O R M A L   T E R M I N A T I O N
# Done                                                 31-May-2023 15:54:04
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Import FEBio results

if runFlag==1 %i.e. a succesful run

    % Importing nodal displacements from a log file
    dataStruct=importFEBio_logfile(fullfile(savePath,febioLogFileName_disp),0,1);

    %Access data
    N_disp_mat=dataStruct.data; %Displacement
    timeVec=dataStruct.time; %Time

    %Create deformed coordinate set
    V_DEF=N_disp_mat+repmat(V,[1 1 size(N_disp_mat,3)]);

Plotting the simulated results using anim8 to visualize and animate deformations

    DN_magnitude=sqrt(sum(N_disp_mat(:,:,end).^2,2)); %Current displacement magnitude

    % Create basic view and store graphics handle to initiate animation
    hf=cFigure; %Open figure
    gtitle([febioFebFileNamePart,': Press play to animate']);
    title('Displacement magnitude [mm]','Interpreter','Latex')
    hp=gpatch(Fb,V_DEF(:,:,end),DN_magnitude,'k',1,2); %Add graphics object to animate
    hp.Marker='.';
    hp.MarkerSize=markerSize2;
    hp.FaceColor='interp';
    gpatch(Fb,V,0.5*ones(1,3),'none',0.25); %A static graphics object

    axisGeom(gca,fontSize);
    colormap(cMap); colorbar;
    caxis([0 max(DN_magnitude)]); caxis manual;
    axis(axisLim(V_DEF)); %Set axis limits statically
    view(140,30);
    camlight headlight;

    % Set up animation features
    animStruct.Time=timeVec; %The time vector
    for qt=1:1:size(N_disp_mat,3) %Loop over time increments
        DN_magnitude=sqrt(sum(N_disp_mat(:,:,qt).^2,2)); %Current displacement magnitude

        %Set entries in animation structure
        animStruct.Handles{qt}=[hp hp]; %Handles of objects to animate
        animStruct.Props{qt}={'Vertices','CData'}; %Properties of objects to animate
        animStruct.Set{qt}={V_DEF(:,:,qt),DN_magnitude}; %Property values for to set in order to animate
    end
    anim8(hf,animStruct); %Initiate animation feature
    drawnow;

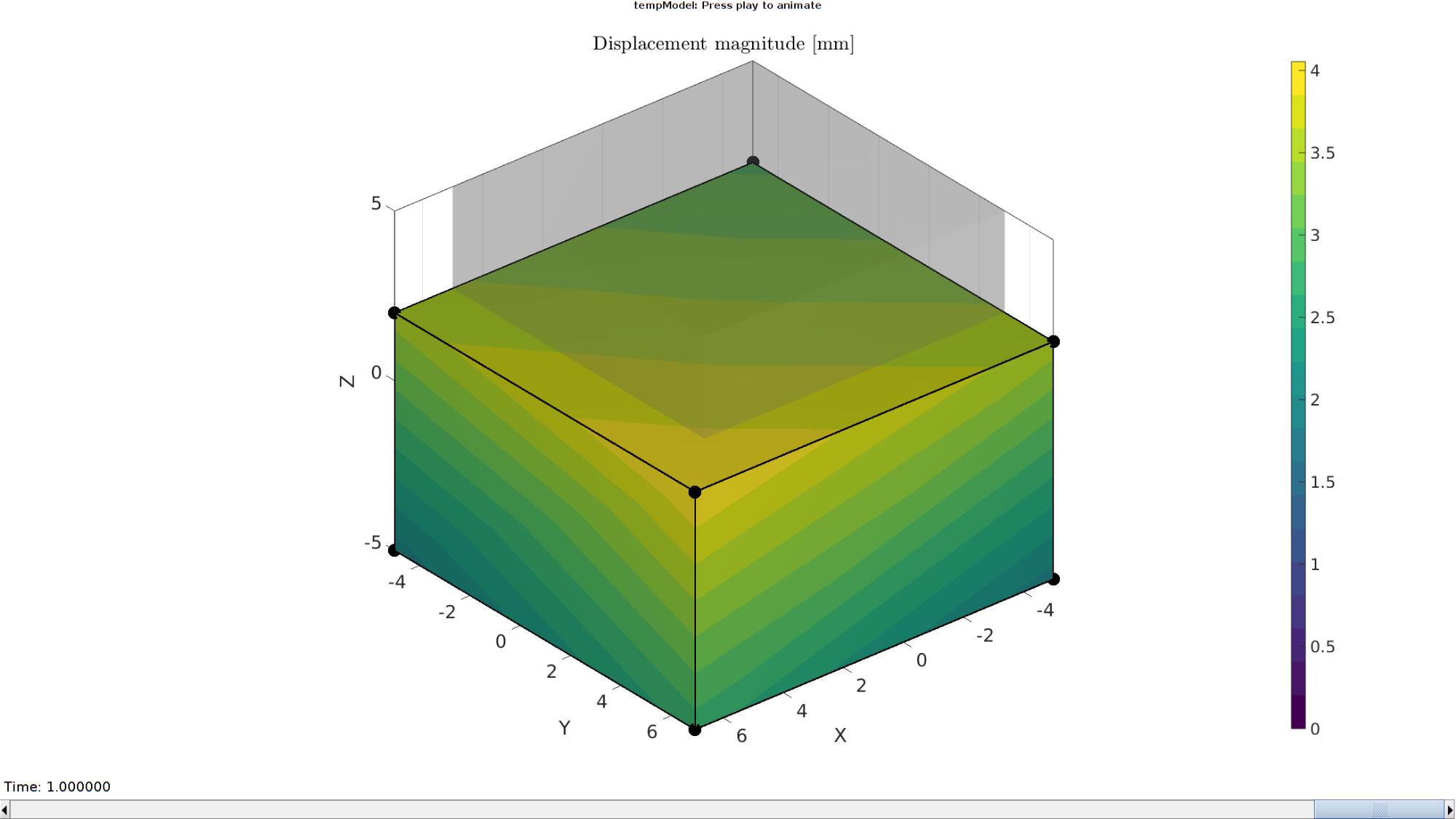
Importing element stress from a log file

    dataStruct=importFEBio_logfile(fullfile(savePath,febioLogFileName_stress),0,1);

    %Access data
    E_stress_mat=dataStruct.data;

Importing element stretch from a log file

    dataStruct=importFEBio_logfile(fullfile(savePath,febioLogFileName_stretch),0,1);

    %Access data
    E_stretch_mat=dataStruct.data;

Plotting the simulated results using anim8 to visualize and animate deformations

    [CV]=faceToVertexMeasure(E,V,E_stress_mat(:,:,end));

    % Create basic view and store graphics handle to initiate animation
    hf=cFigure; %Open figure  /usr/local/MATLAB/R2020a/bin/glnxa64/jcef_helper: symbol lookup error: /lib/x86_64-linux-gnu/libpango-1.0.so.0: undefined symbol: g_ptr_array_copy

    gtitle([febioFebFileNamePart,': Press play to animate']);
    title('$\sigma_{zz}$ [MPa]','Interpreter','Latex')
    hp=gpatch(Fb,V_DEF(:,:,end),CV,'k',1,2); %Add graphics object to animate
    hp.Marker='.';
    hp.MarkerSize=markerSize2;
    hp.FaceColor='interp';
    gpatch(Fb,V,0.5*ones(1,3),'none',0.25); %A static graphics object

    axisGeom(gca,fontSize);
    colormap(cMap); colorbar;
    caxis([min(E_stress_mat(:)) max(E_stress_mat(:))]);
    axis(axisLim(V_DEF)); %Set axis limits statically
    view(140,30);
    camlight headlight;

    % Set up animation features
    animStruct.Time=timeVec; %The time vector
    for qt=1:1:size(N_disp_mat,3) %Loop over time increments

        [CV]=faceToVertexMeasure(E,V,E_stress_mat(:,:,qt));

        %Set entries in animation structure
        animStruct.Handles{qt}=[hp hp]; %Handles of objects to animate
        animStruct.Props{qt}={'Vertices','CData'}; %Properties of objects to animate
        animStruct.Set{qt}={V_DEF(:,:,qt),CV}; %Property values for to set in order to animate
    end
    anim8(hf,animStruct); %Initiate animation feature
    drawnow;

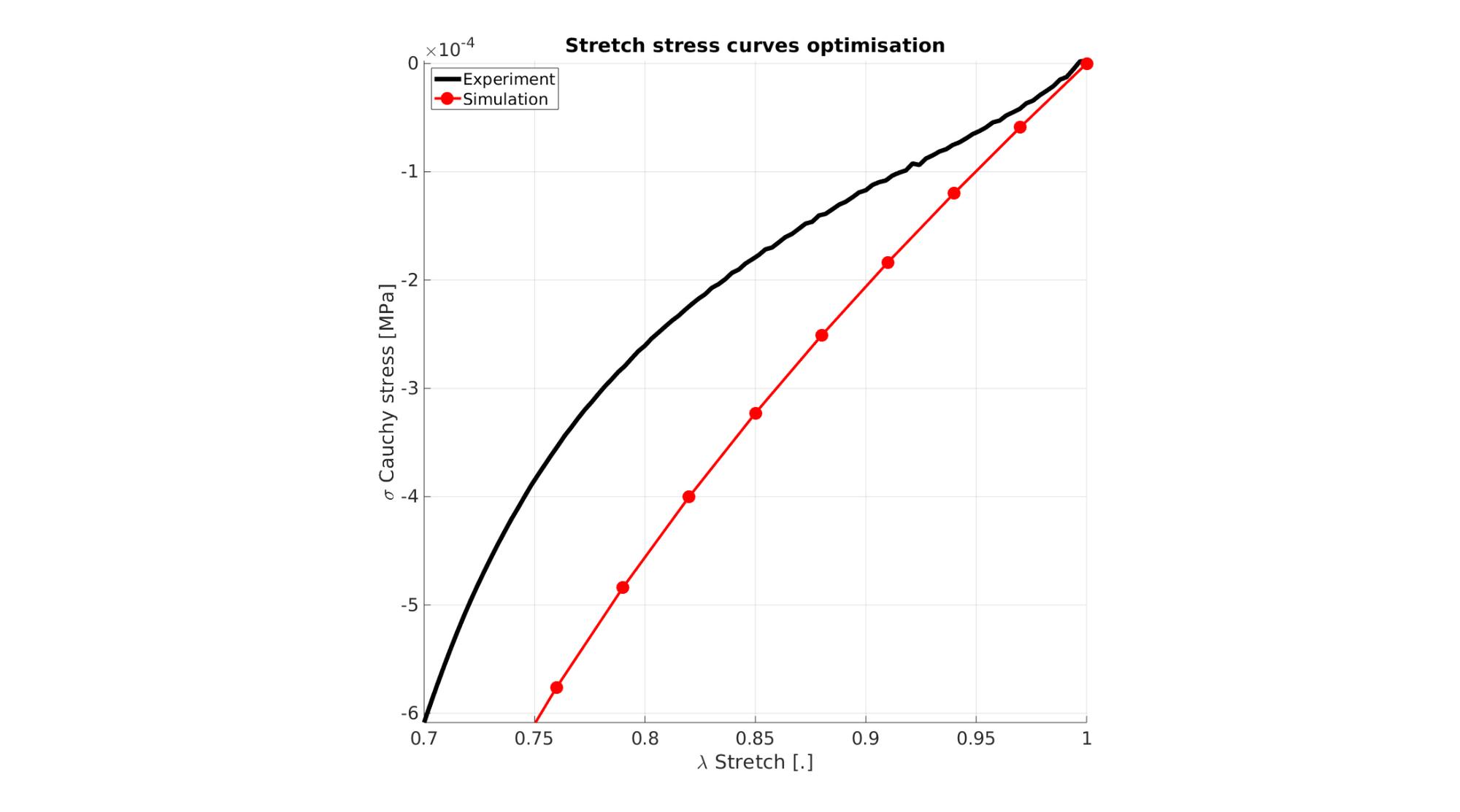
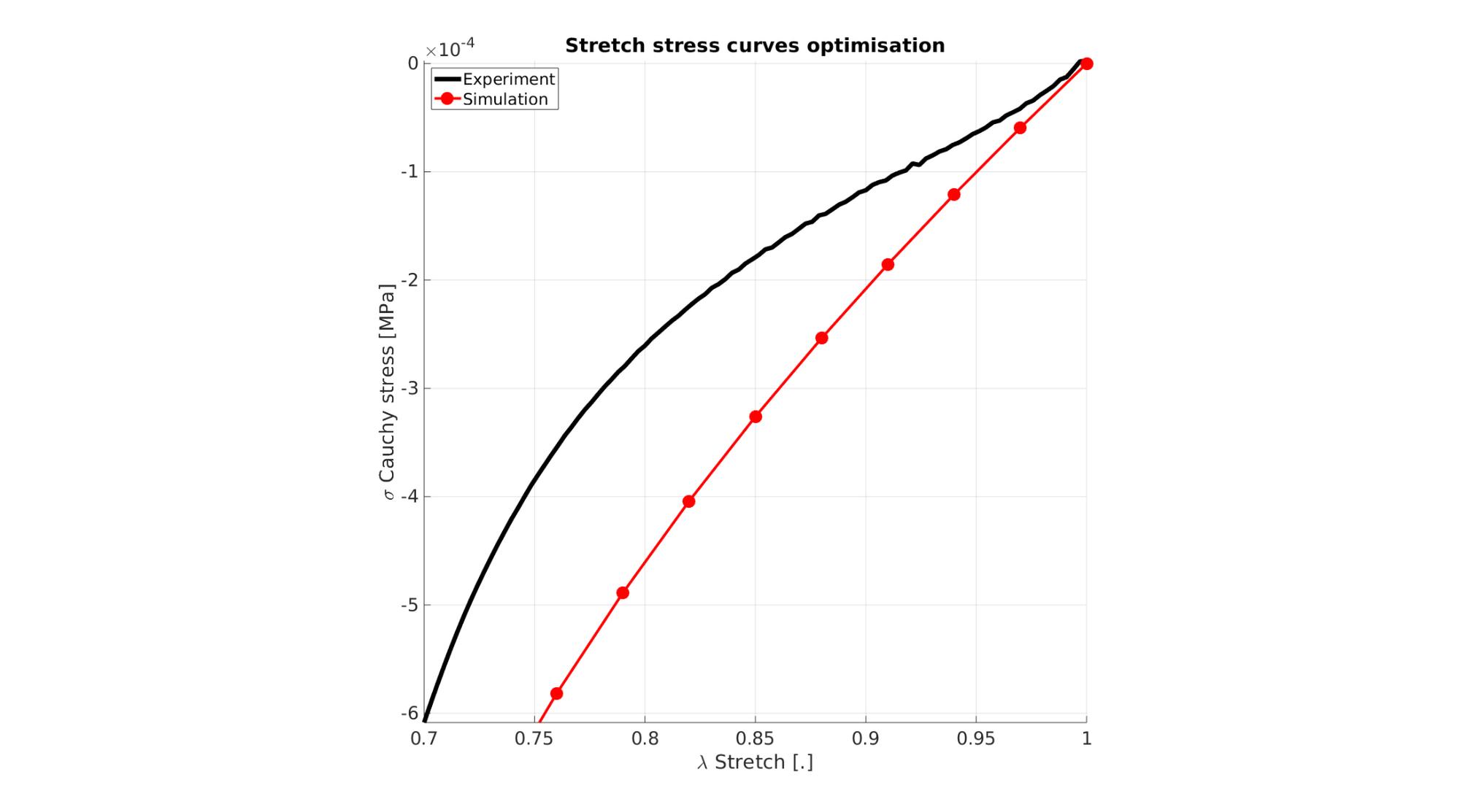
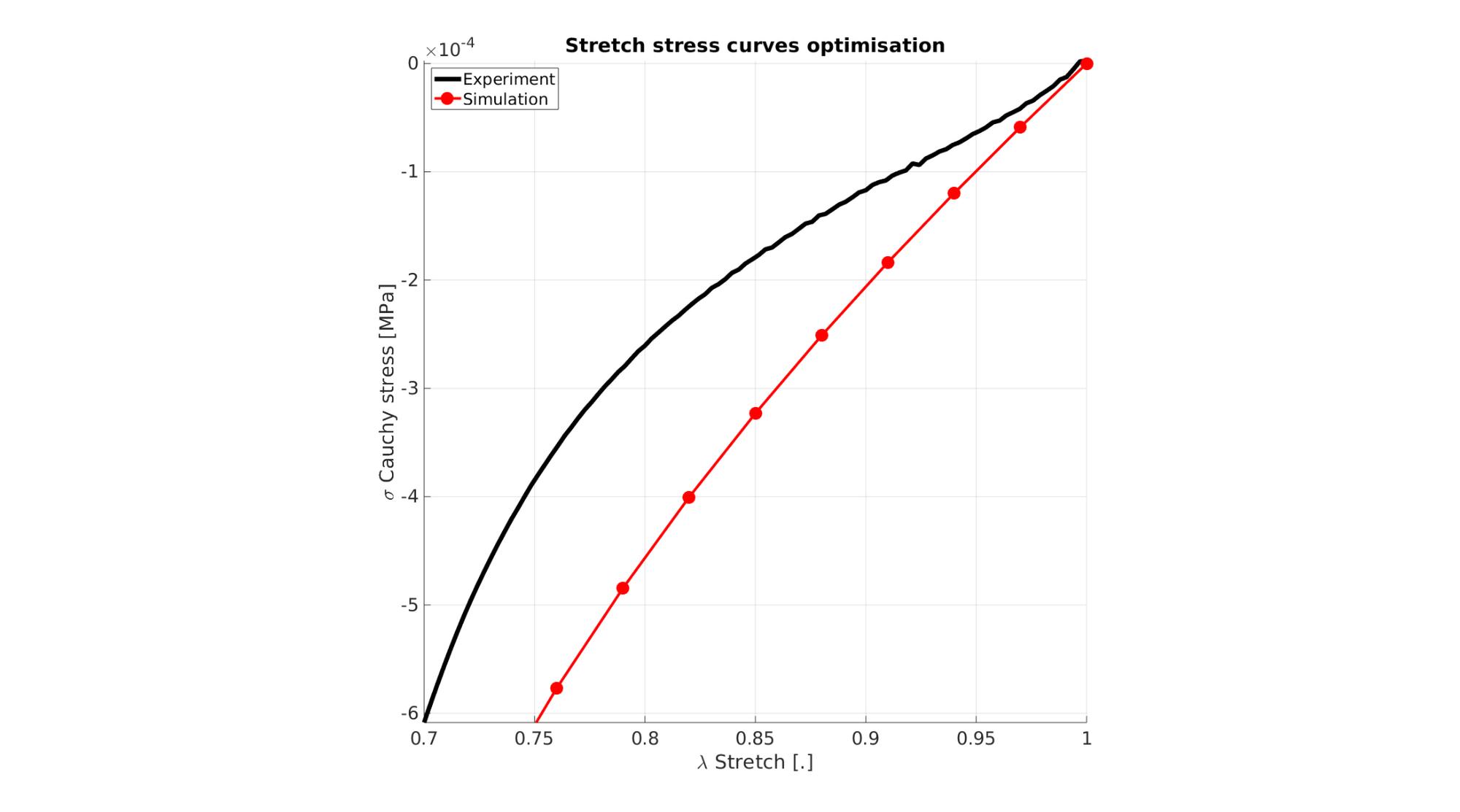
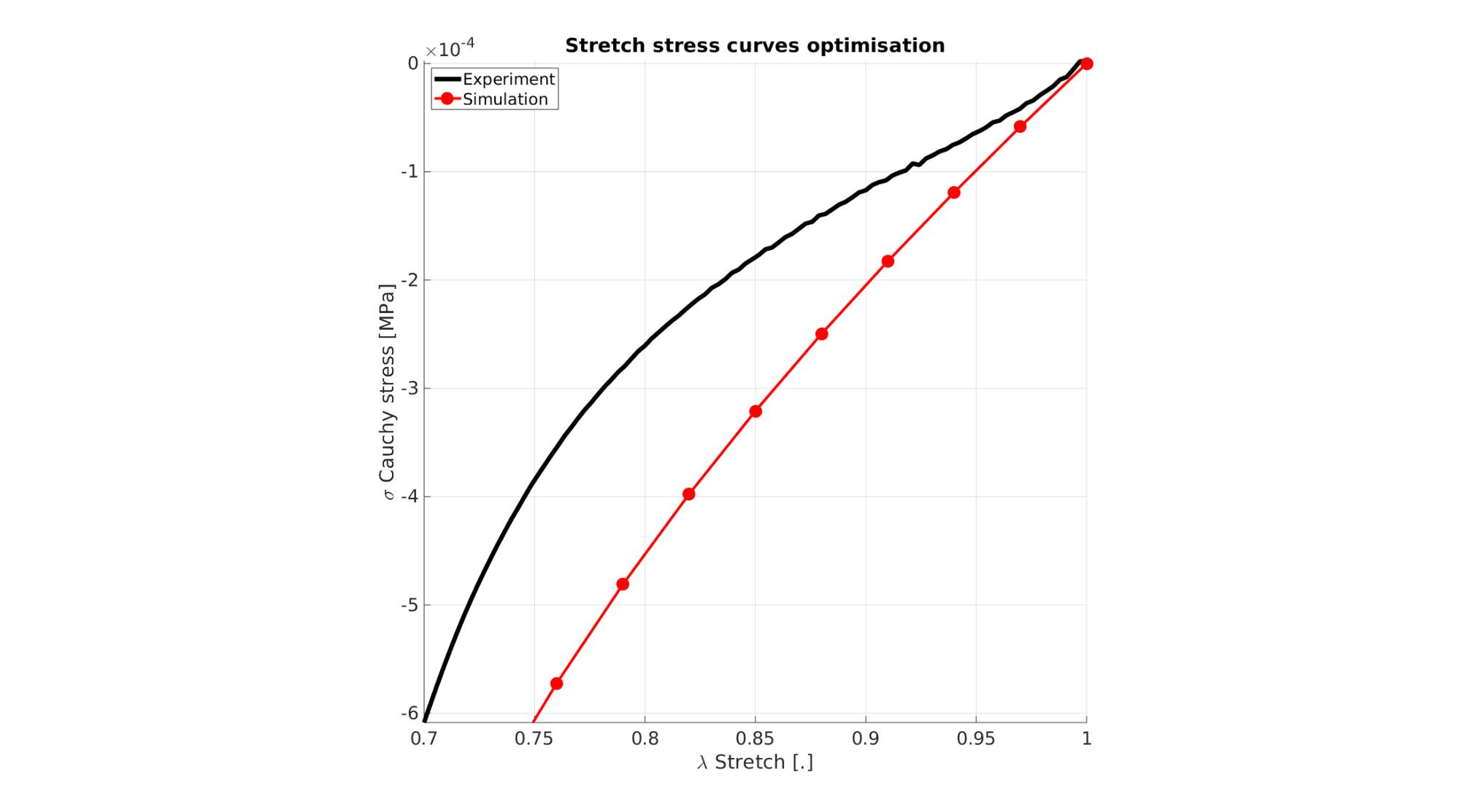
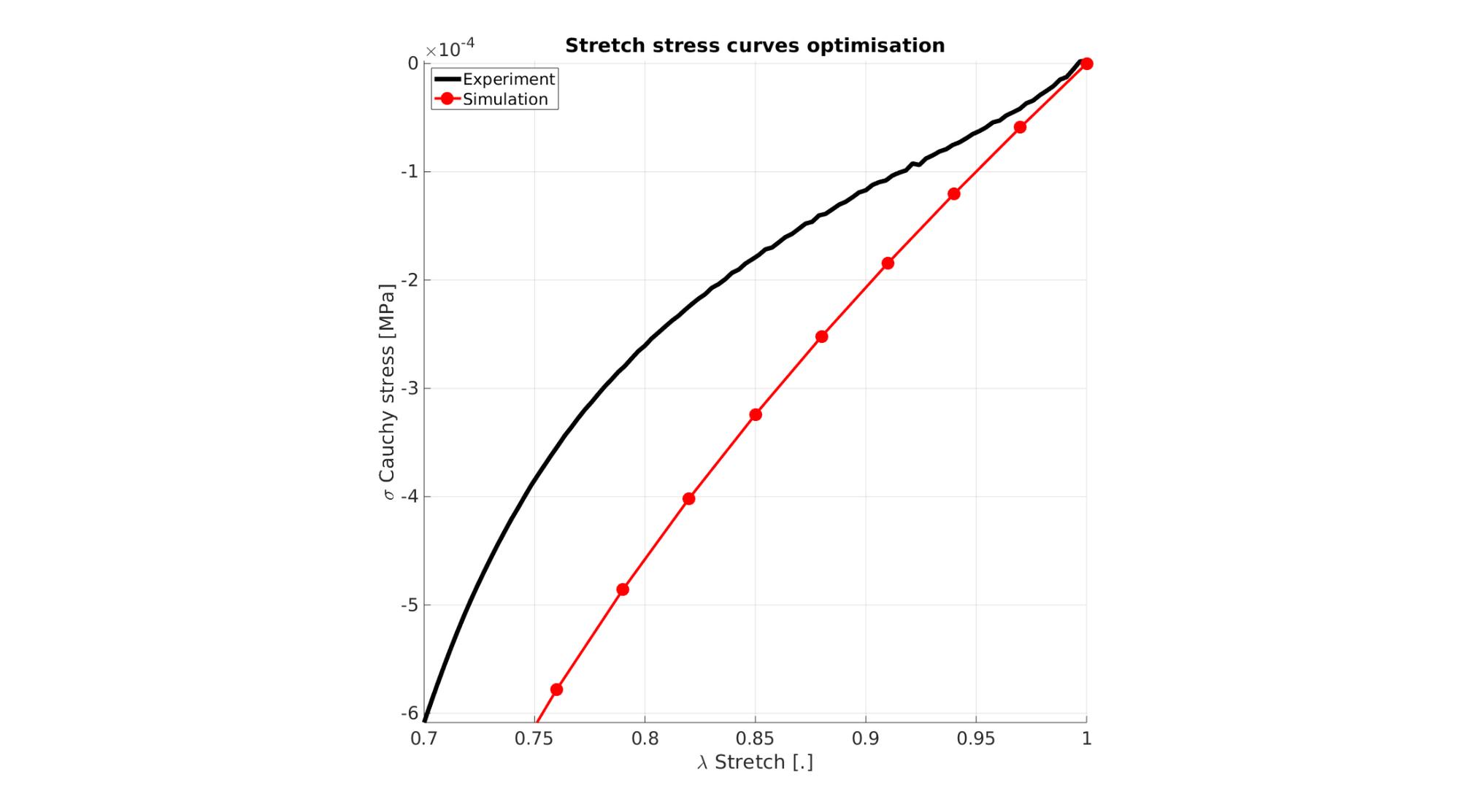
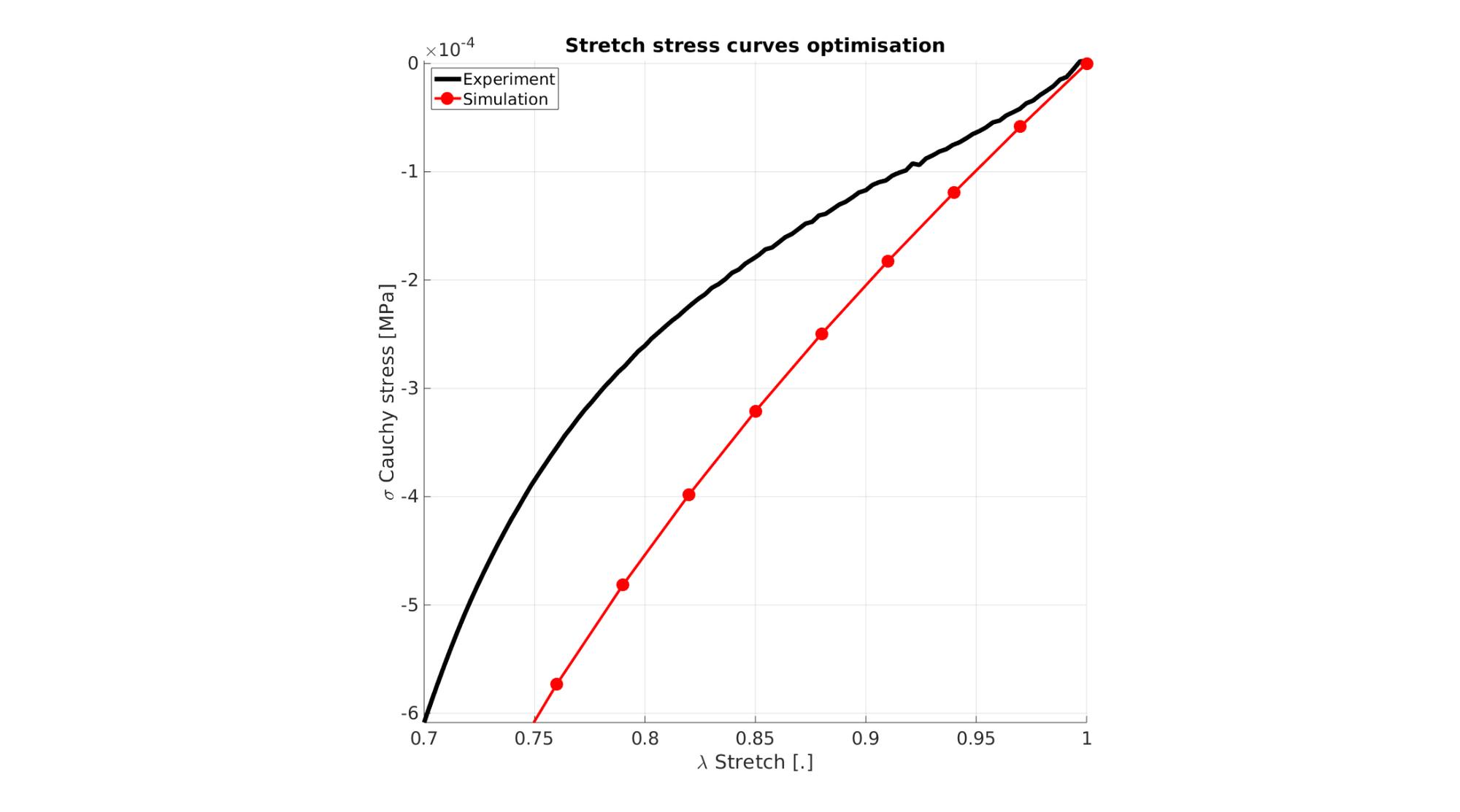
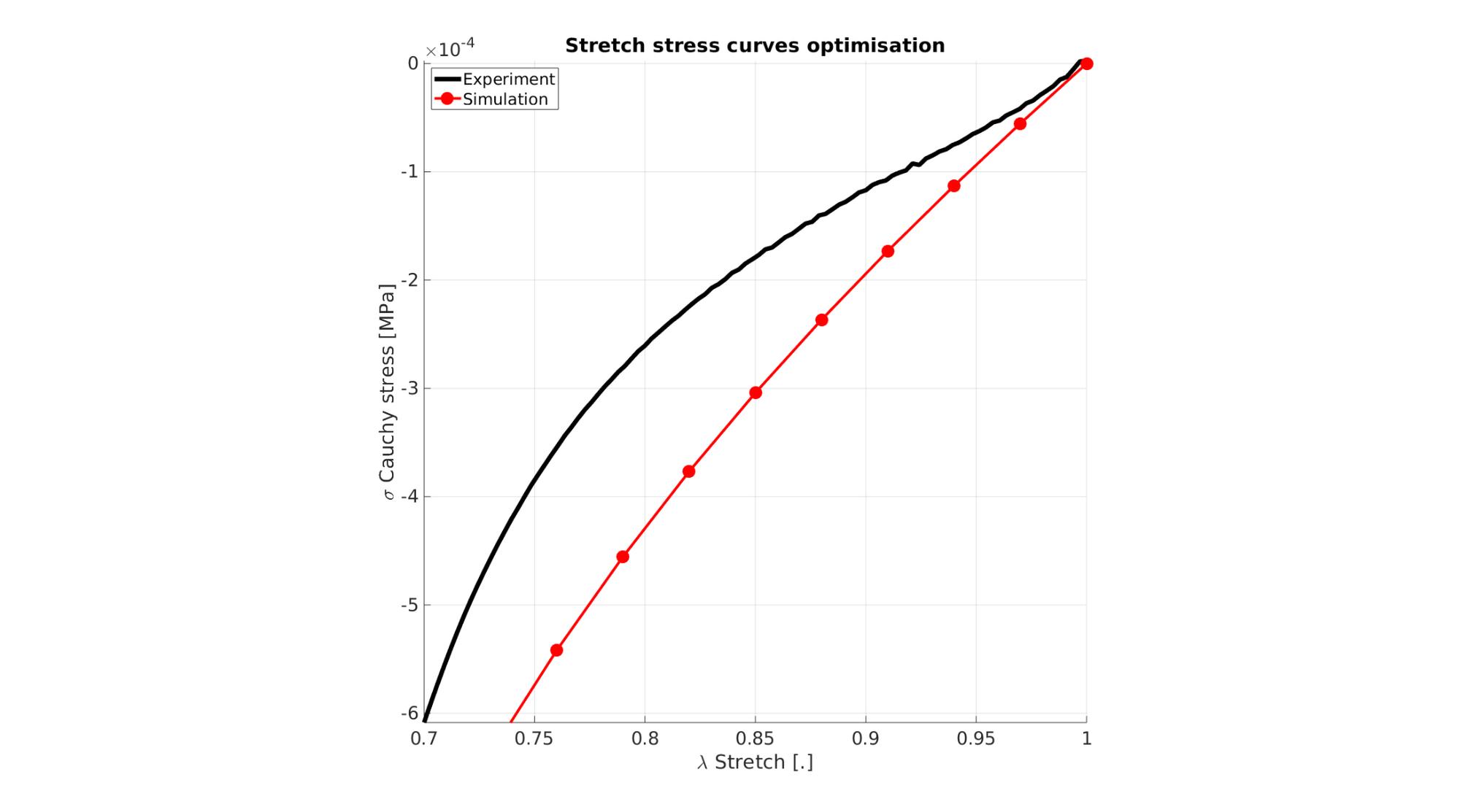
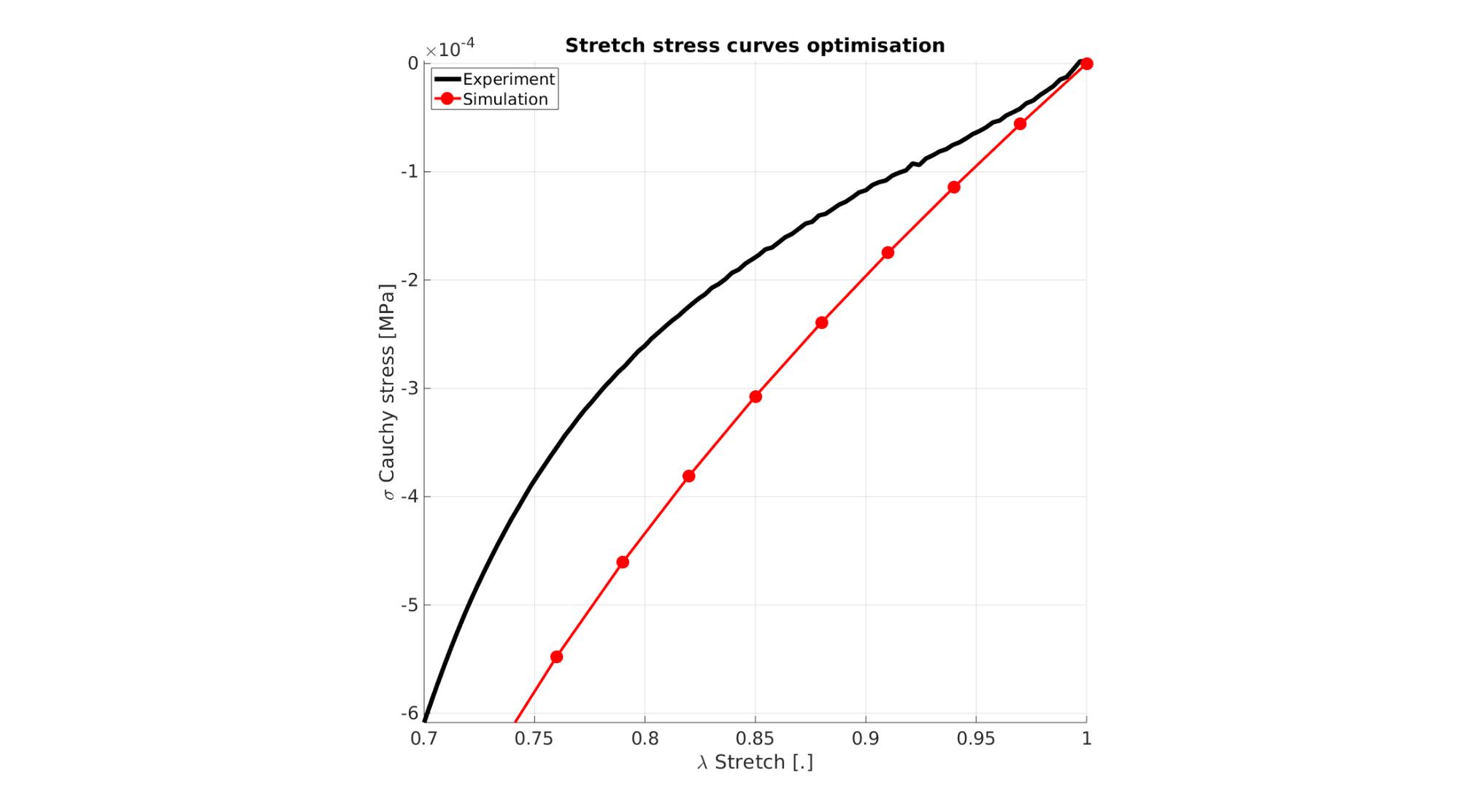
Visualize stretch-stress curve

    stretch_sim=squeeze(mean(E_stretch_mat,1)); % Stretch U_z
    stress_cauchy_sim=squeeze(mean(E_stress_mat,1)); %Cauchy stress sigma_z

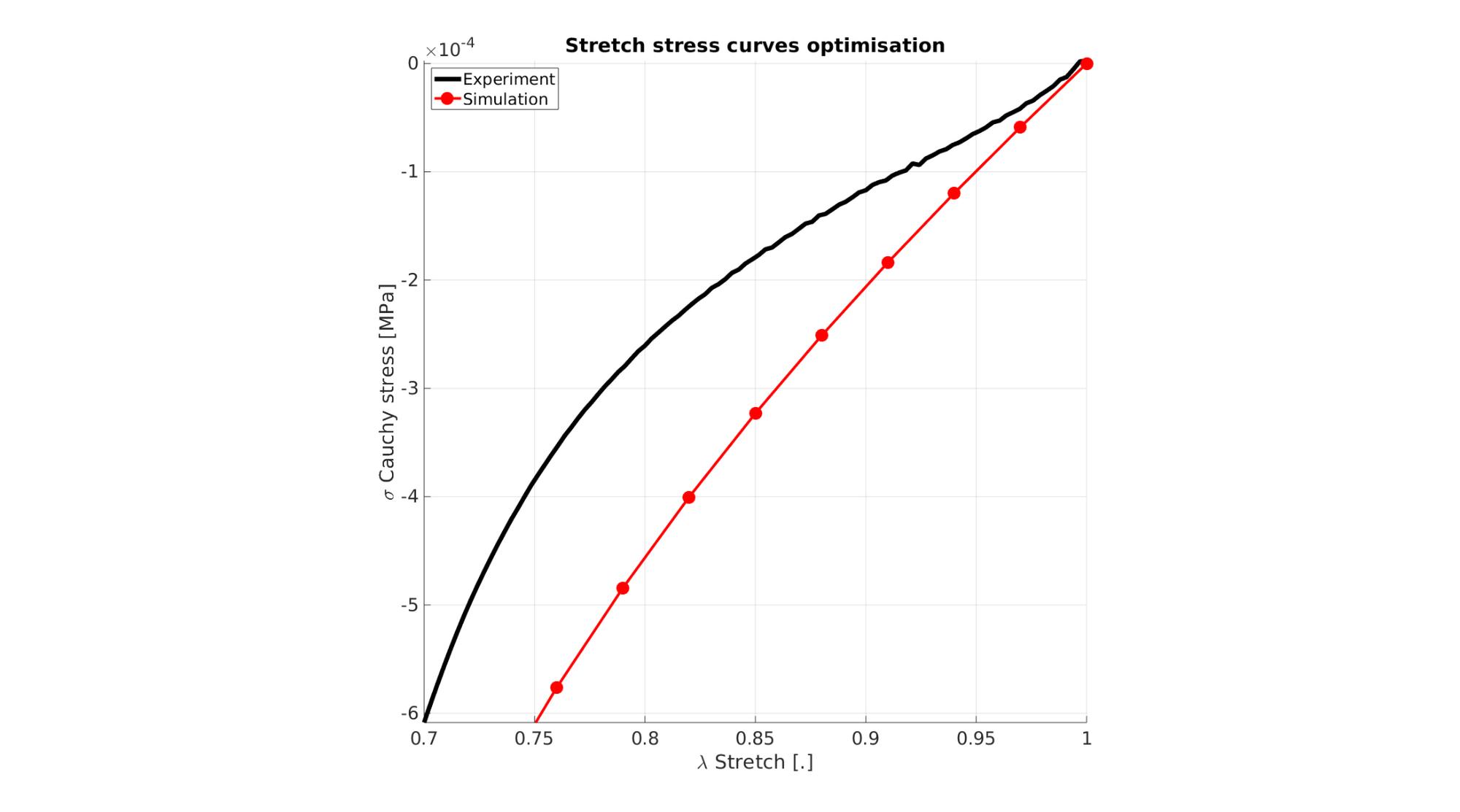
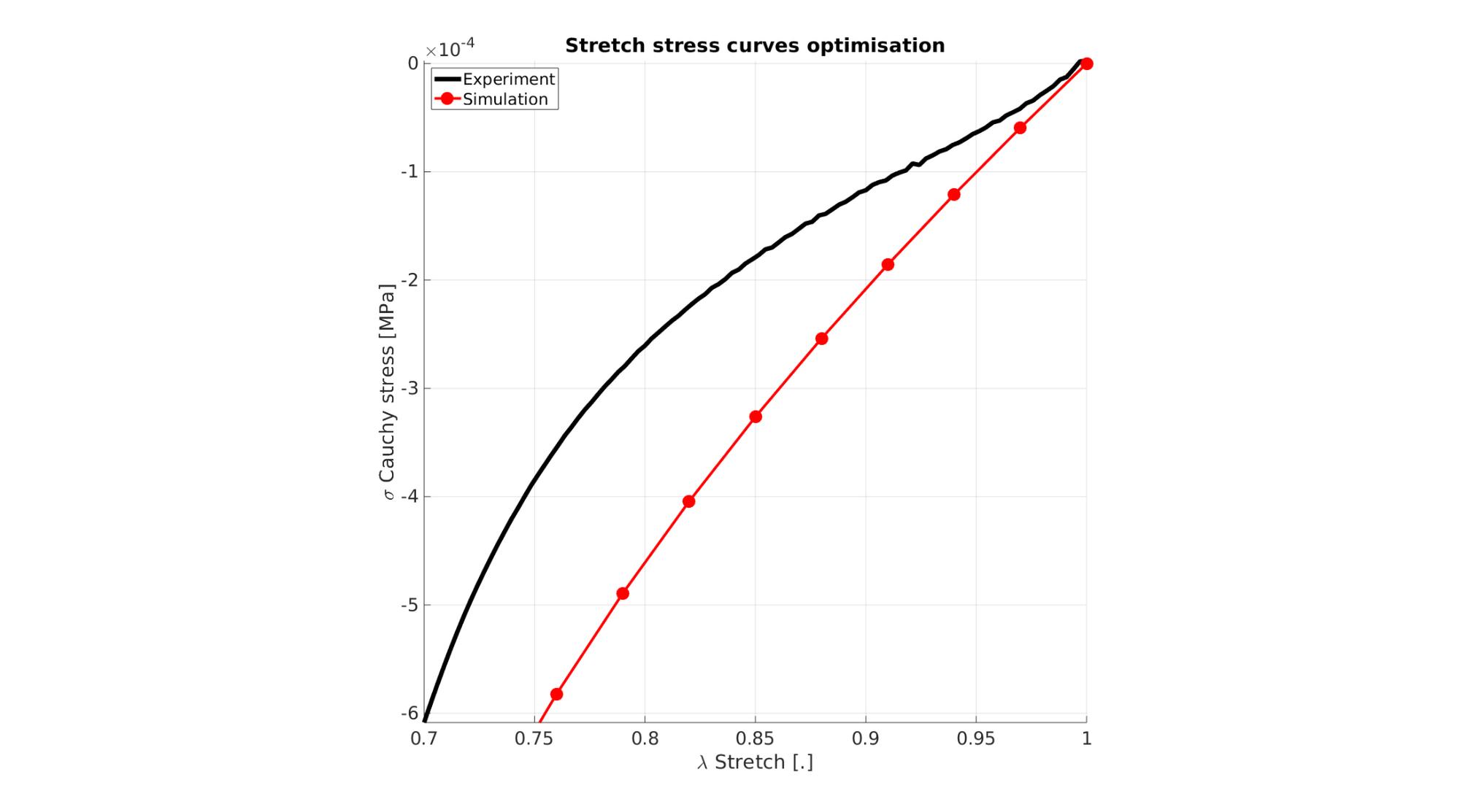
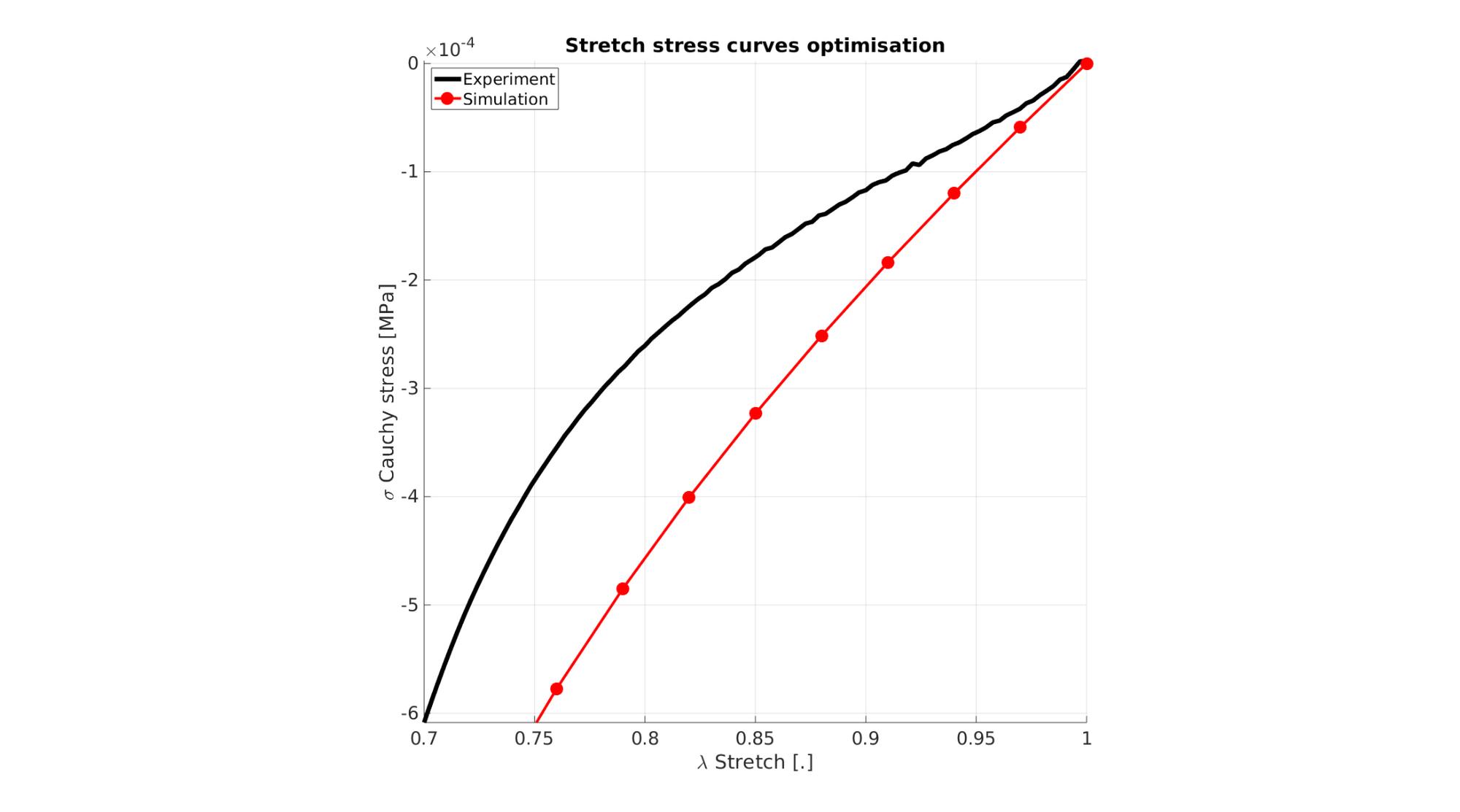
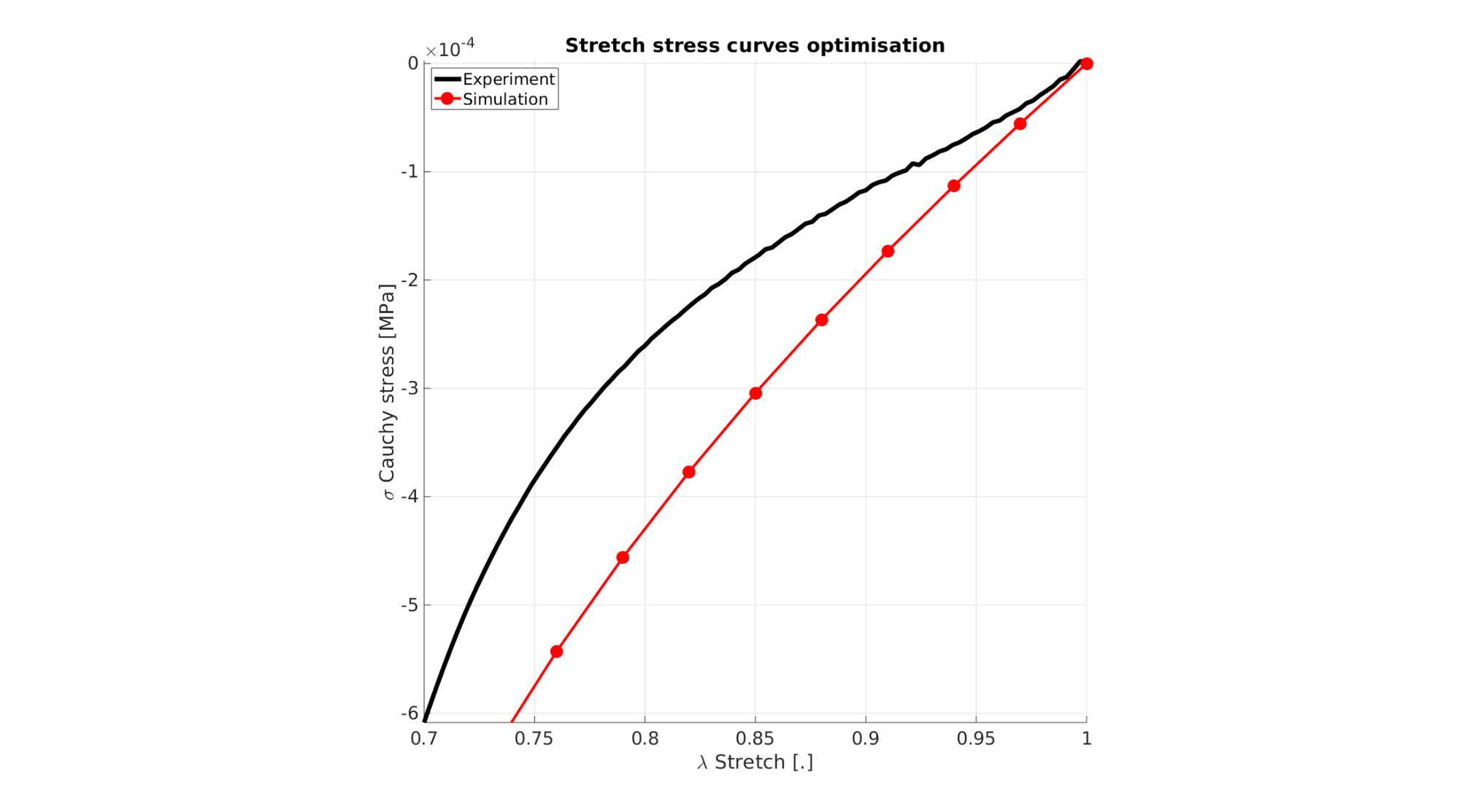
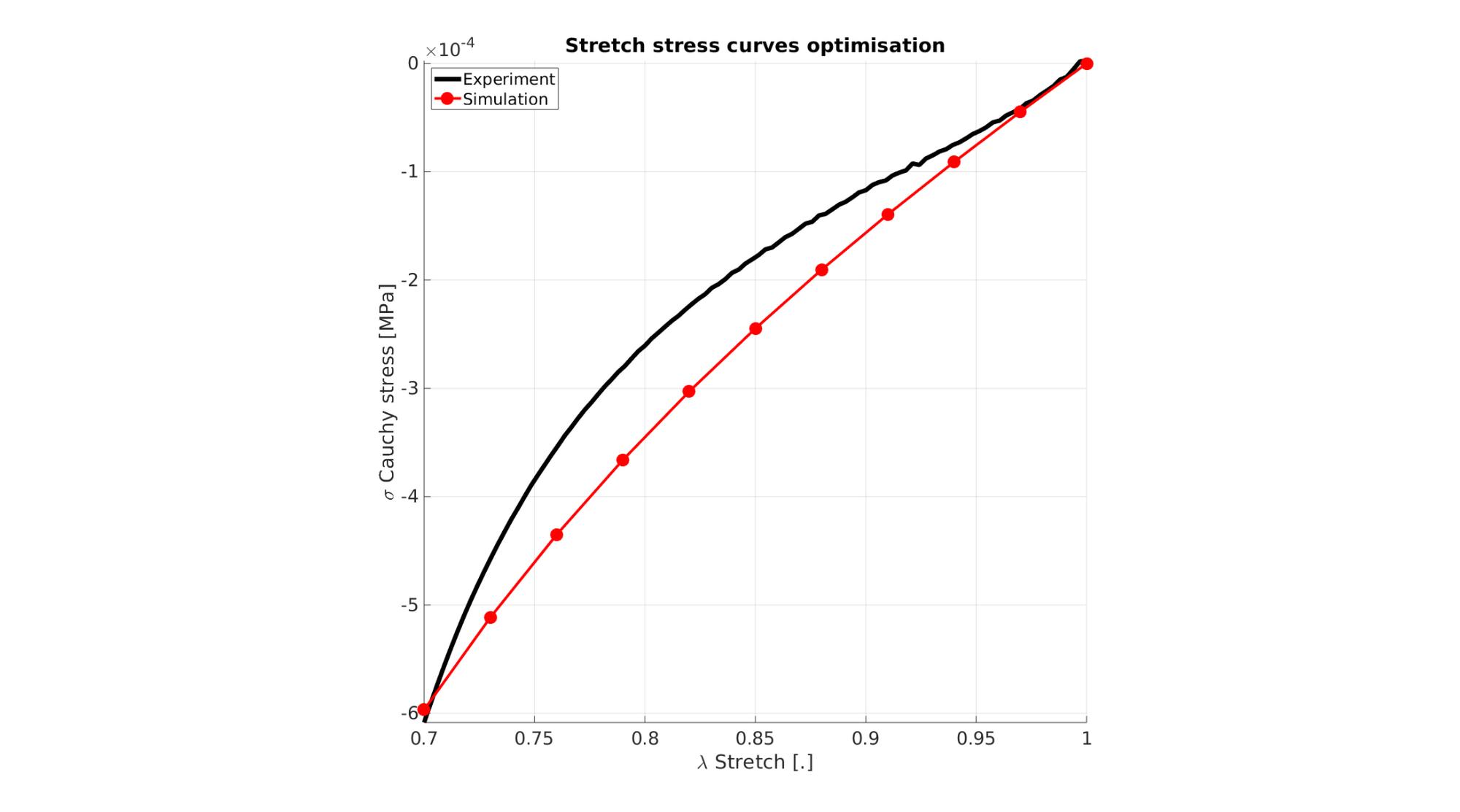
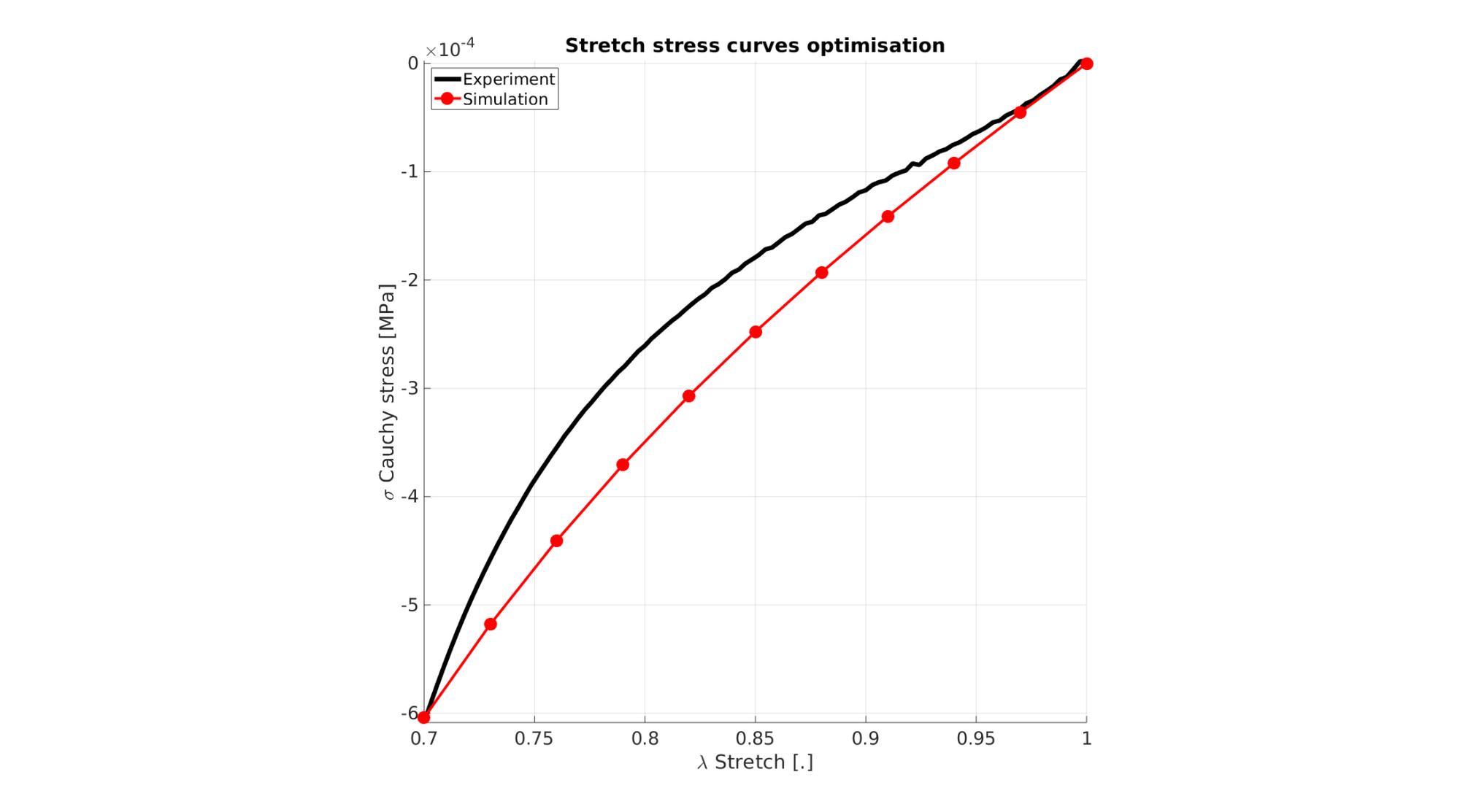
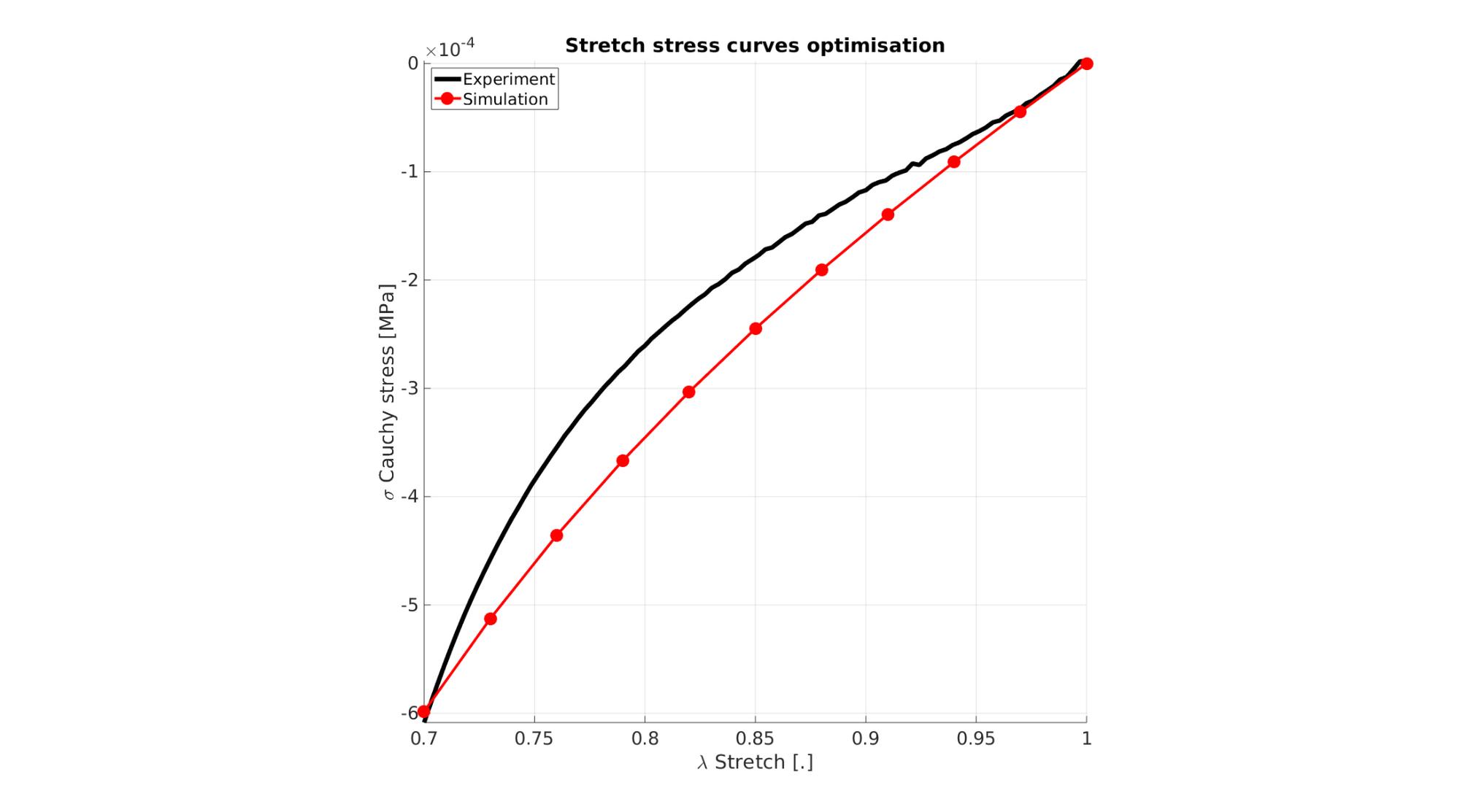
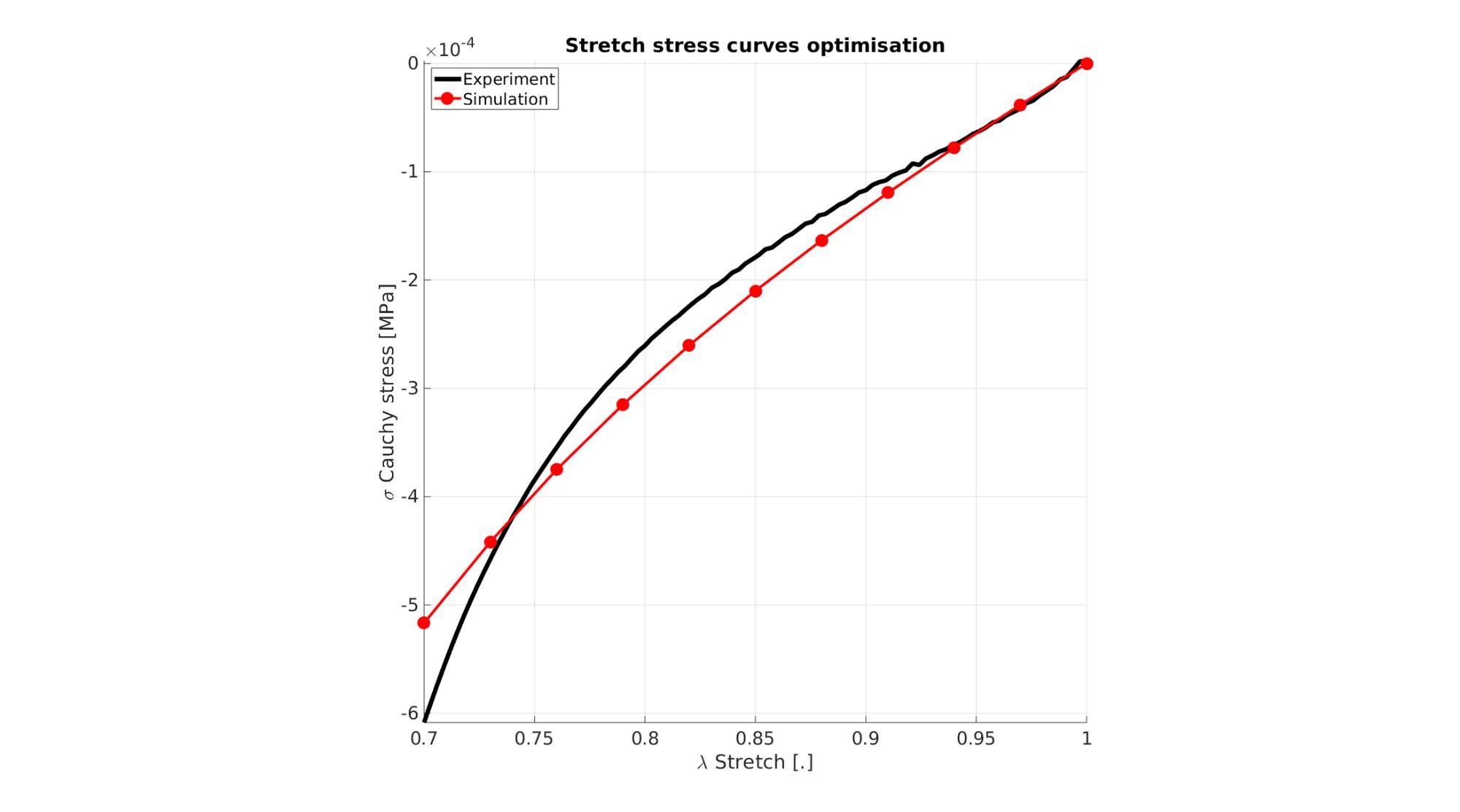
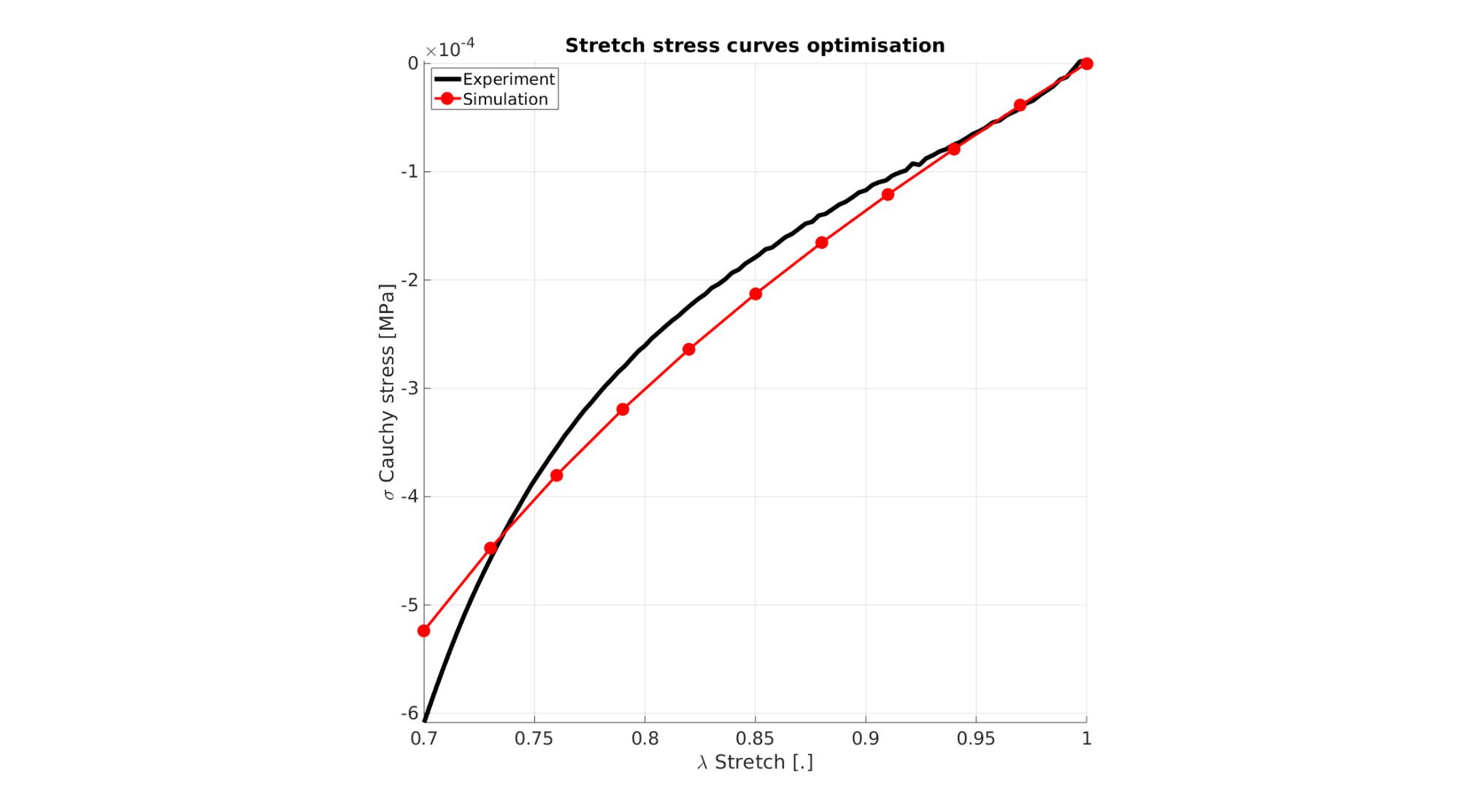
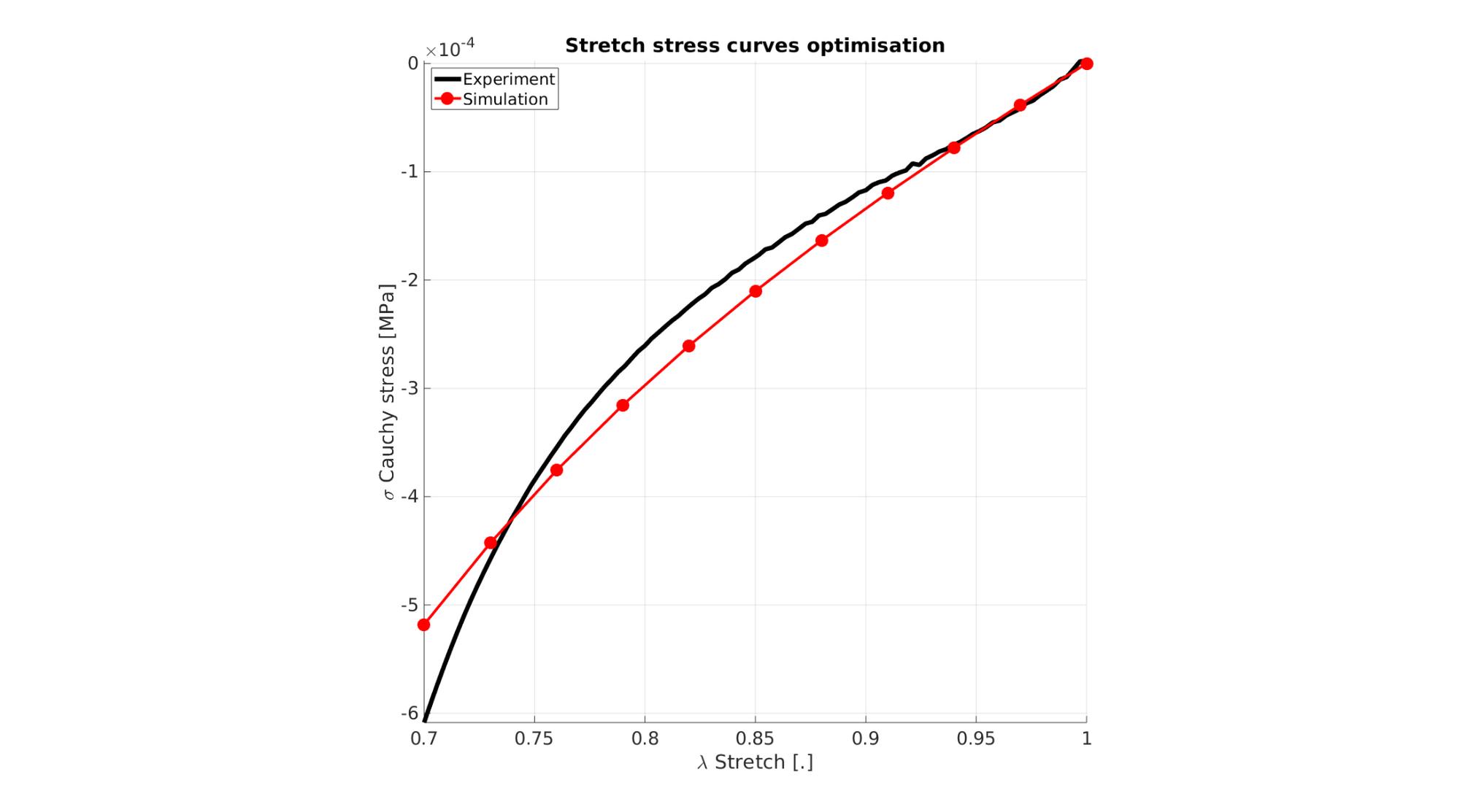
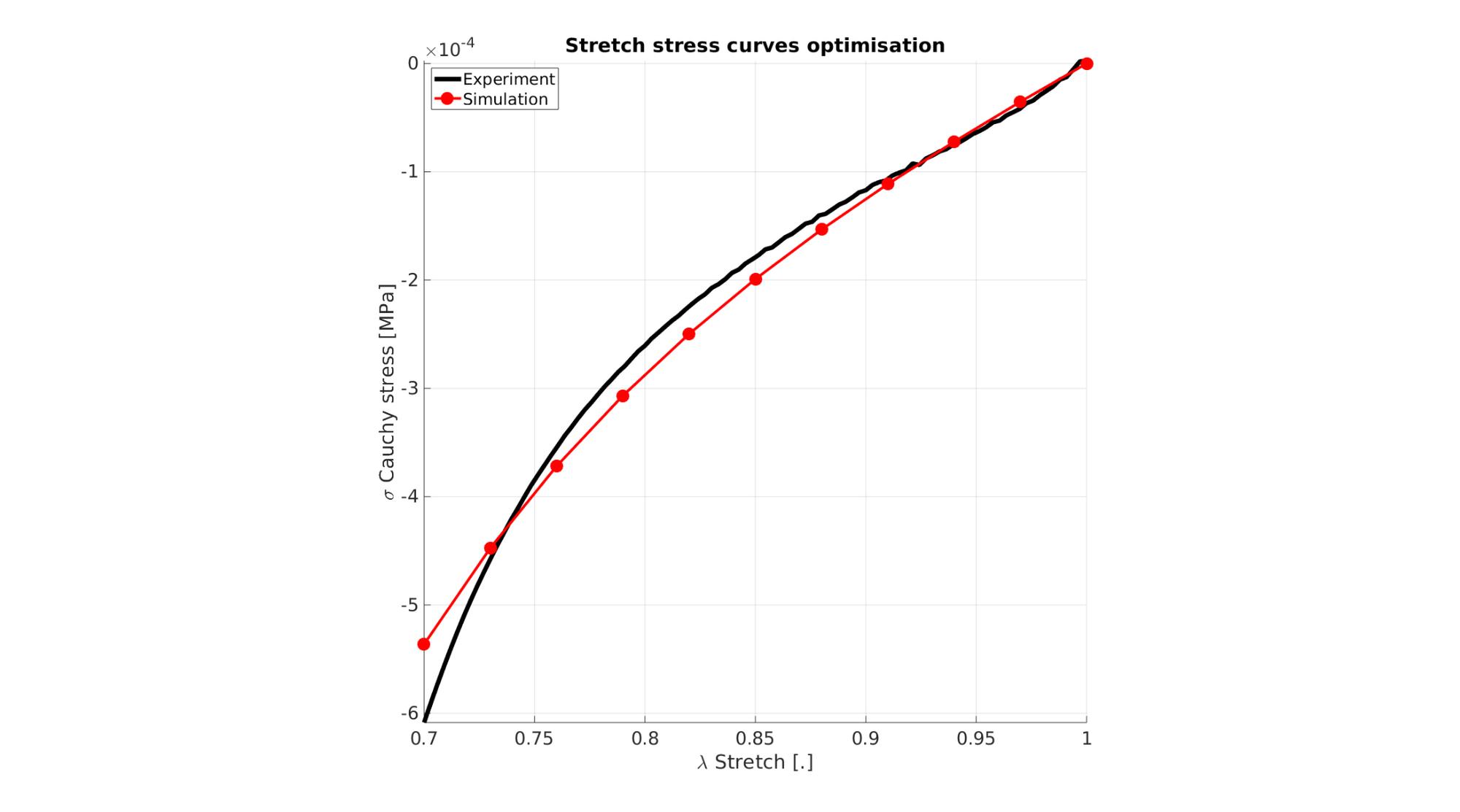
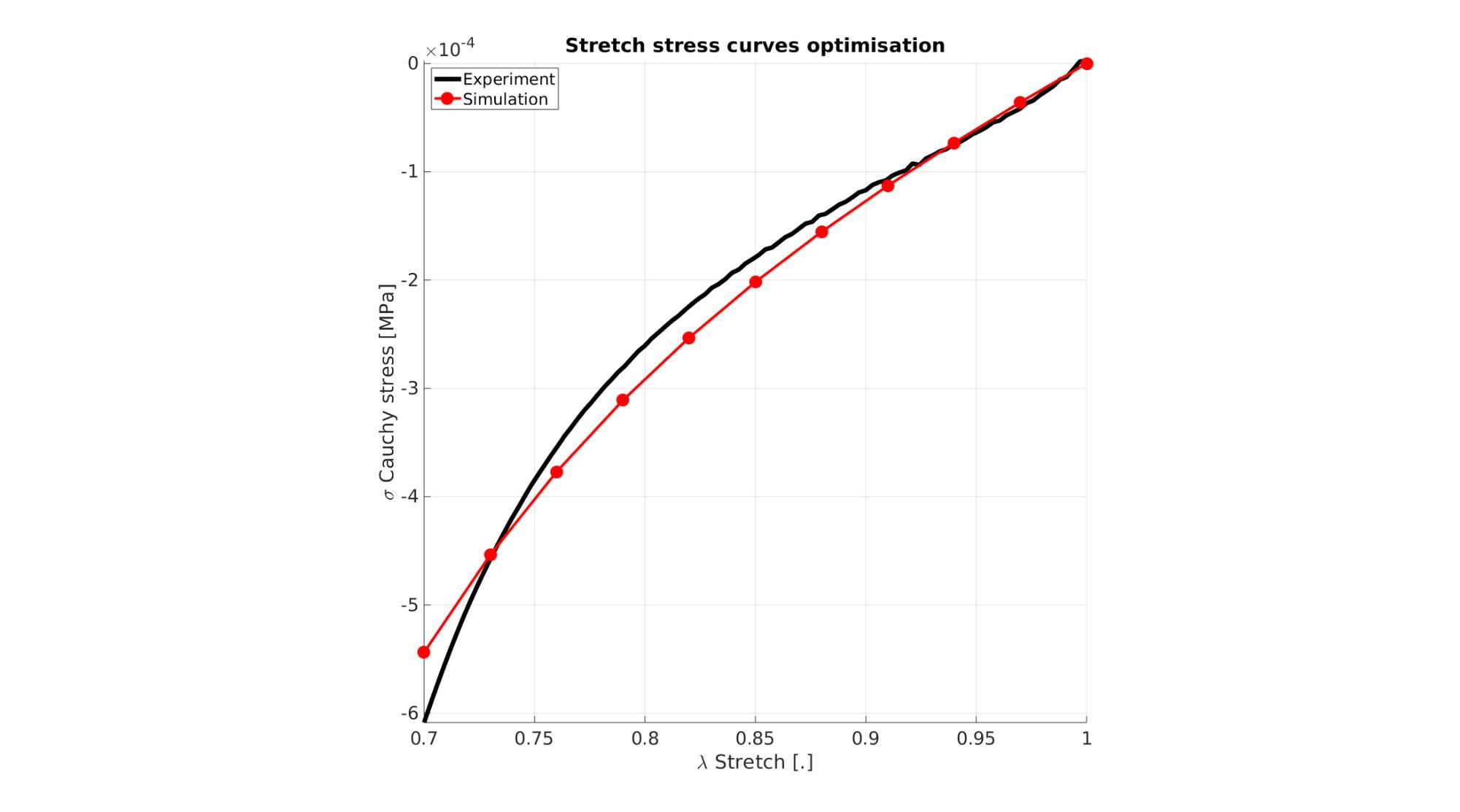
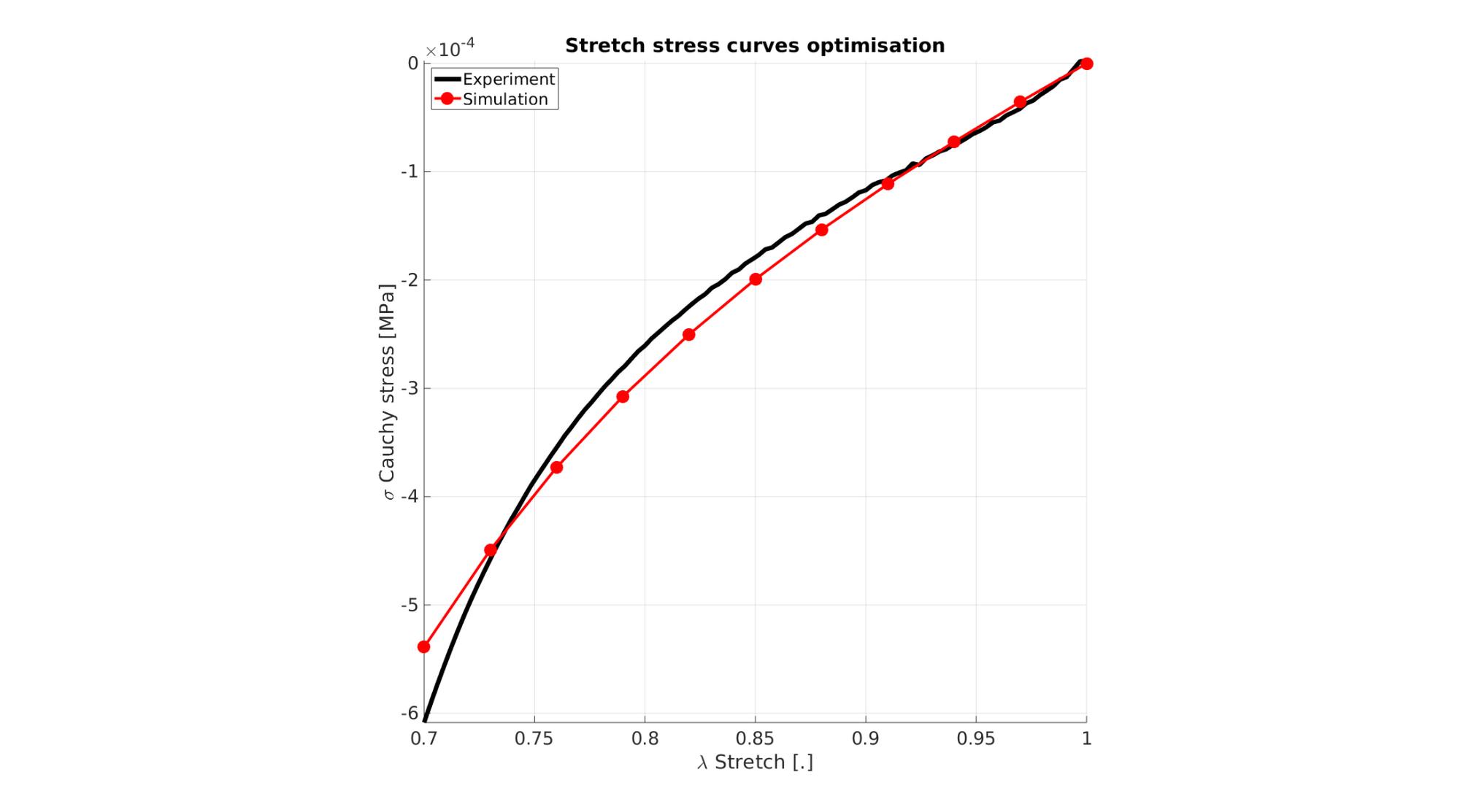
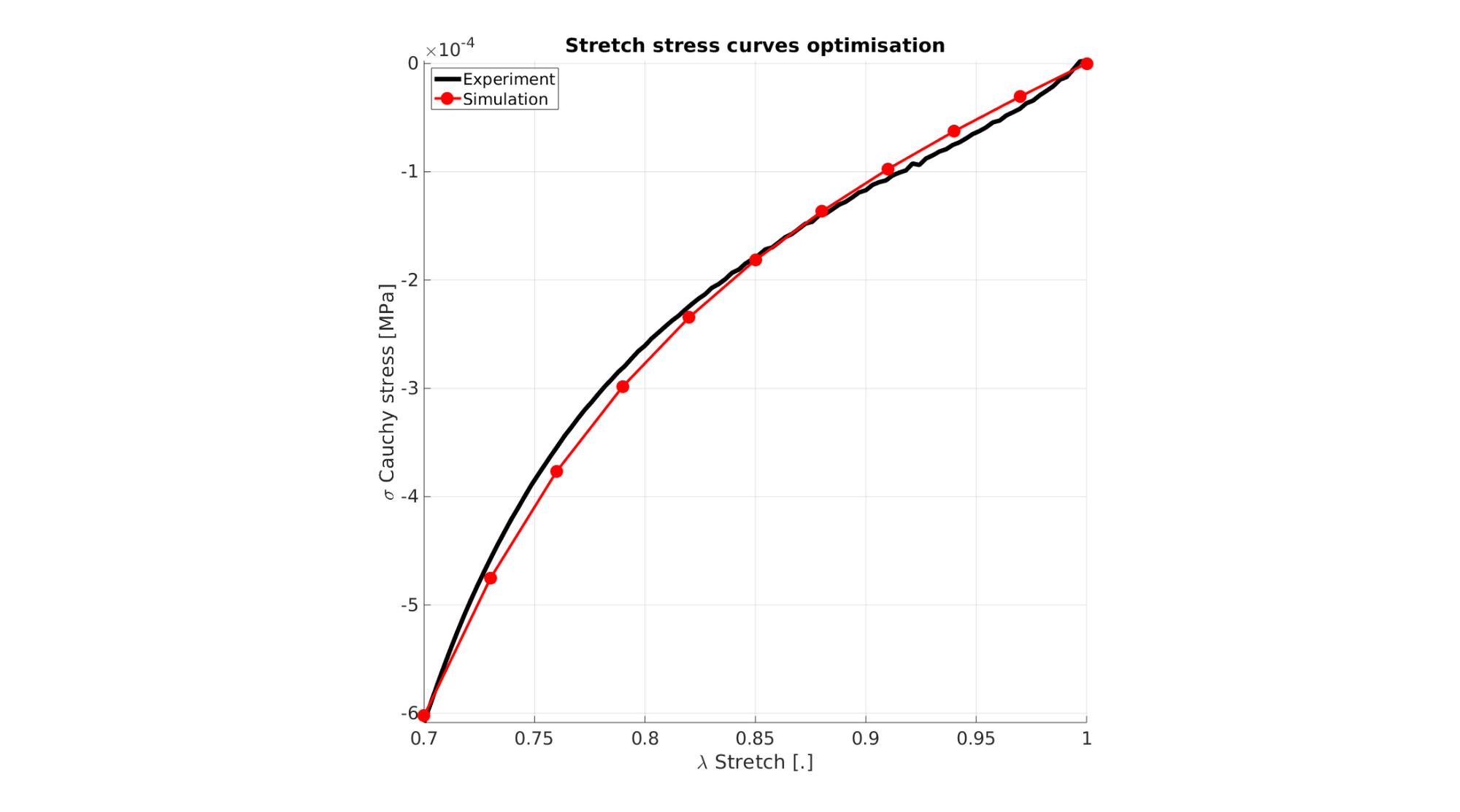
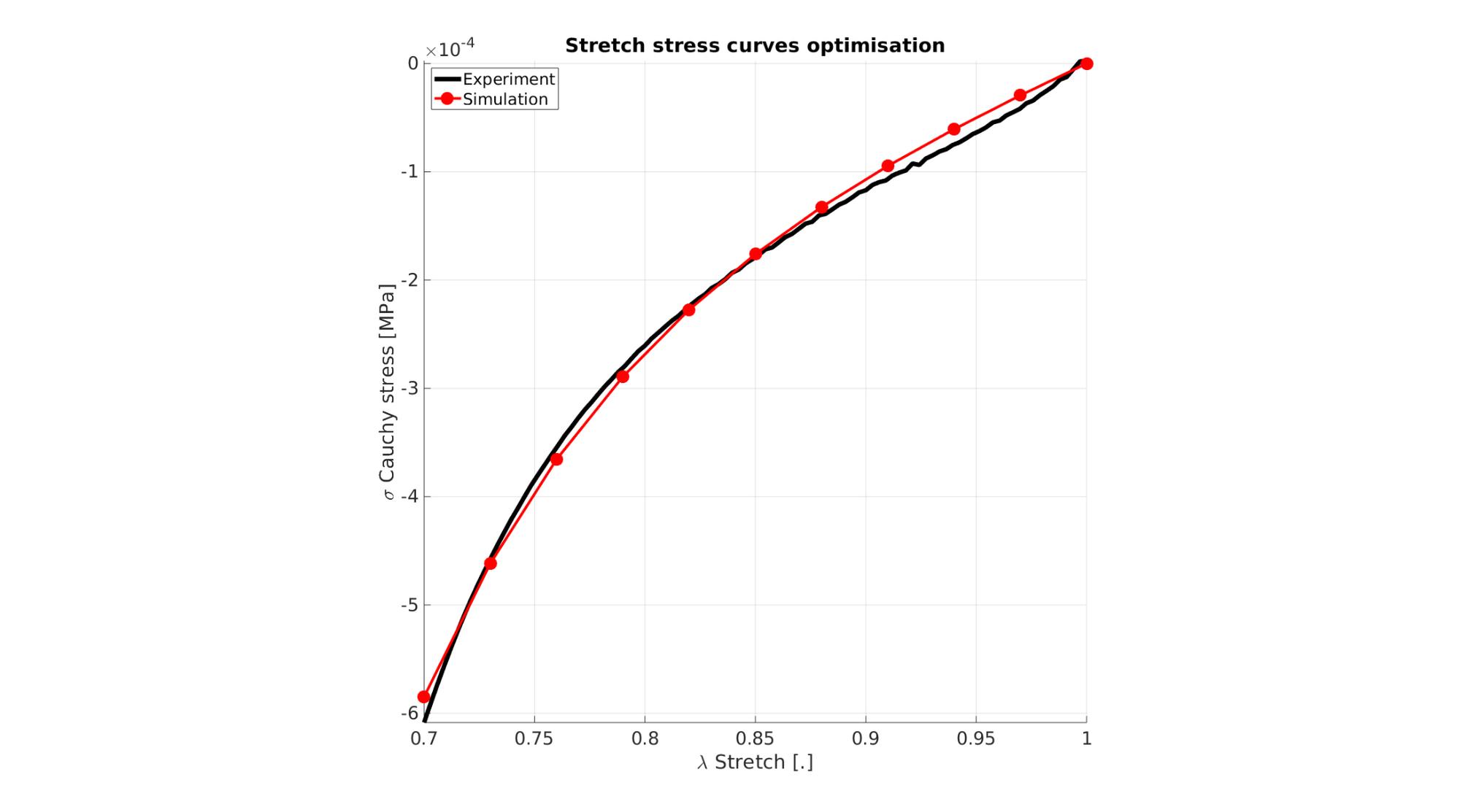
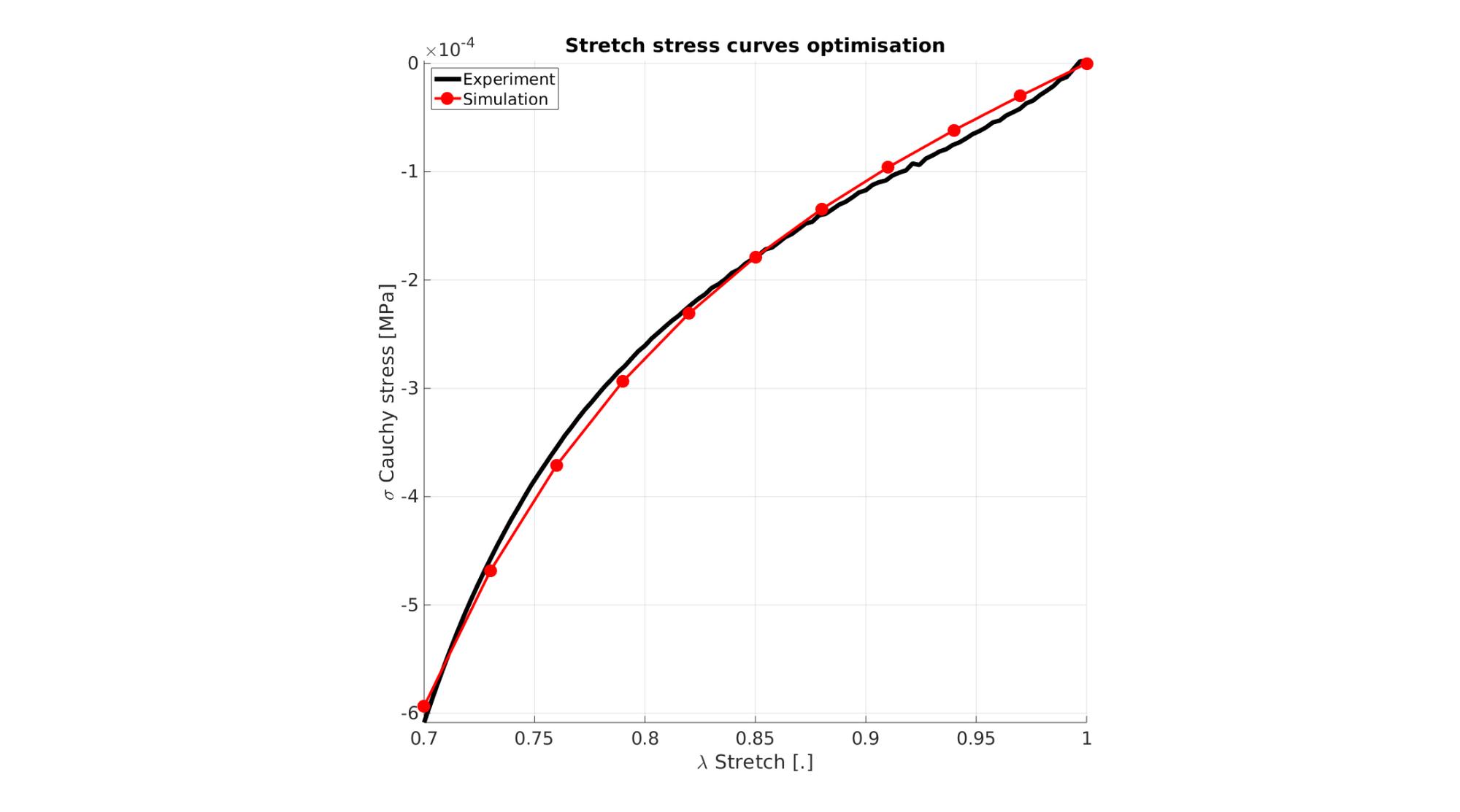
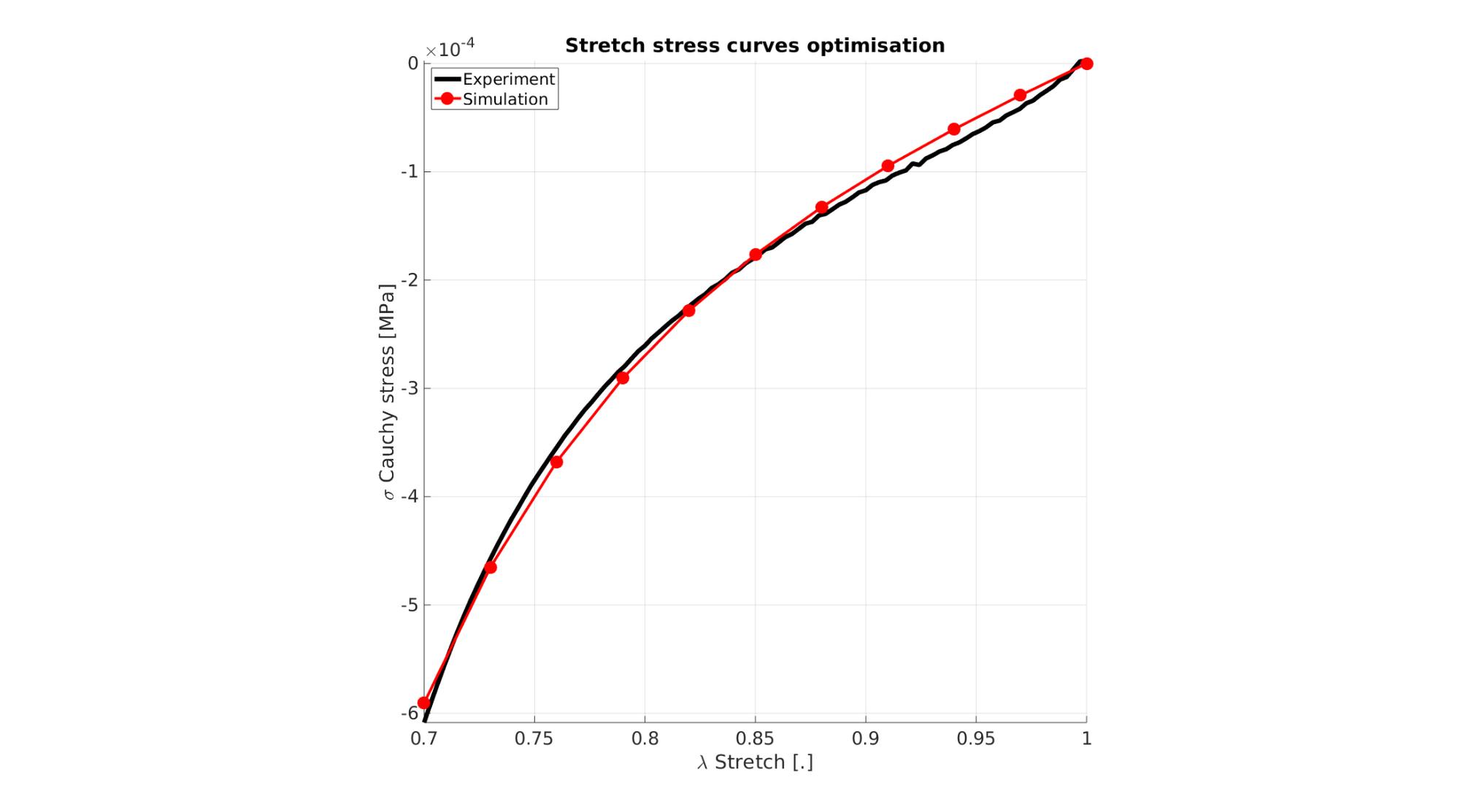
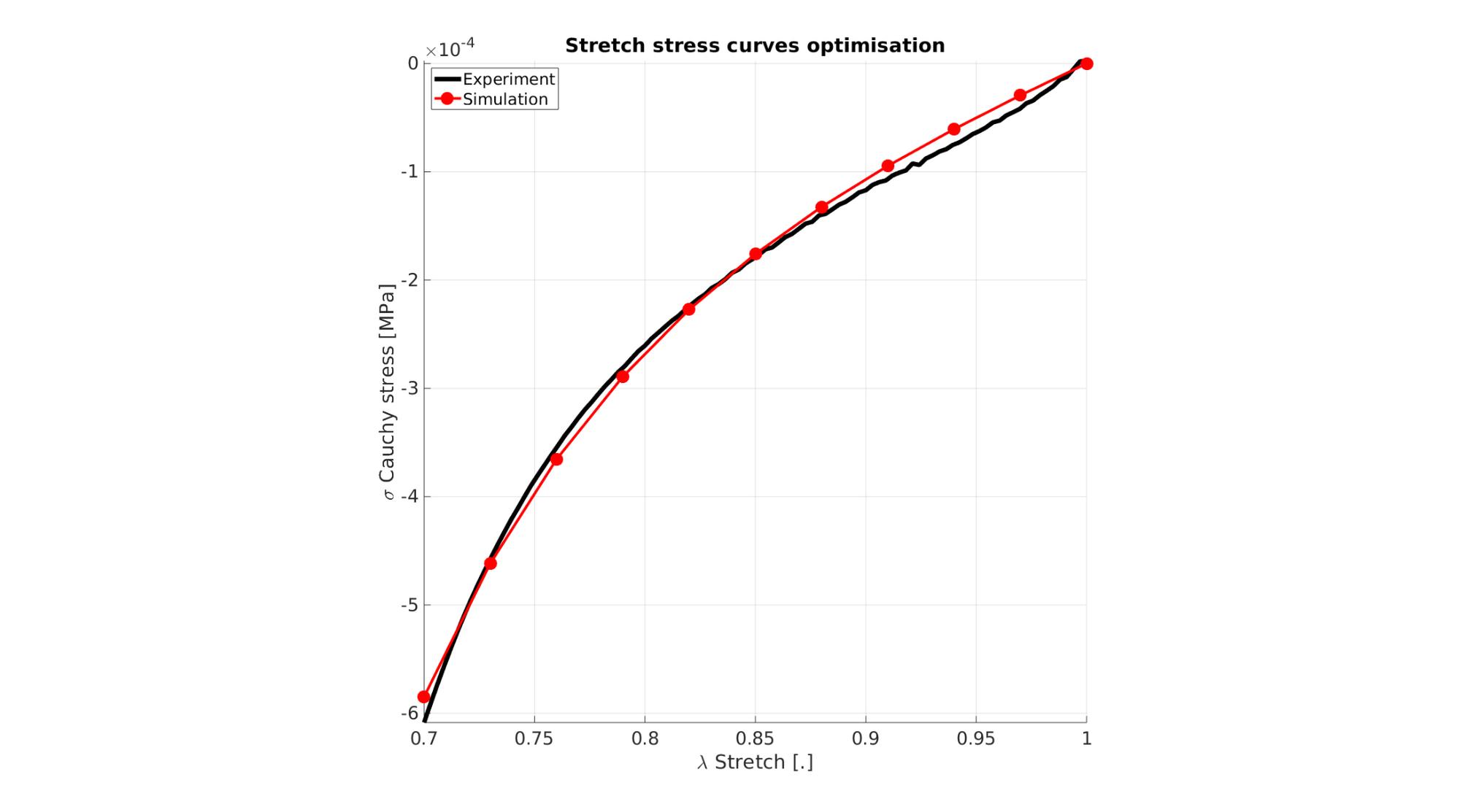
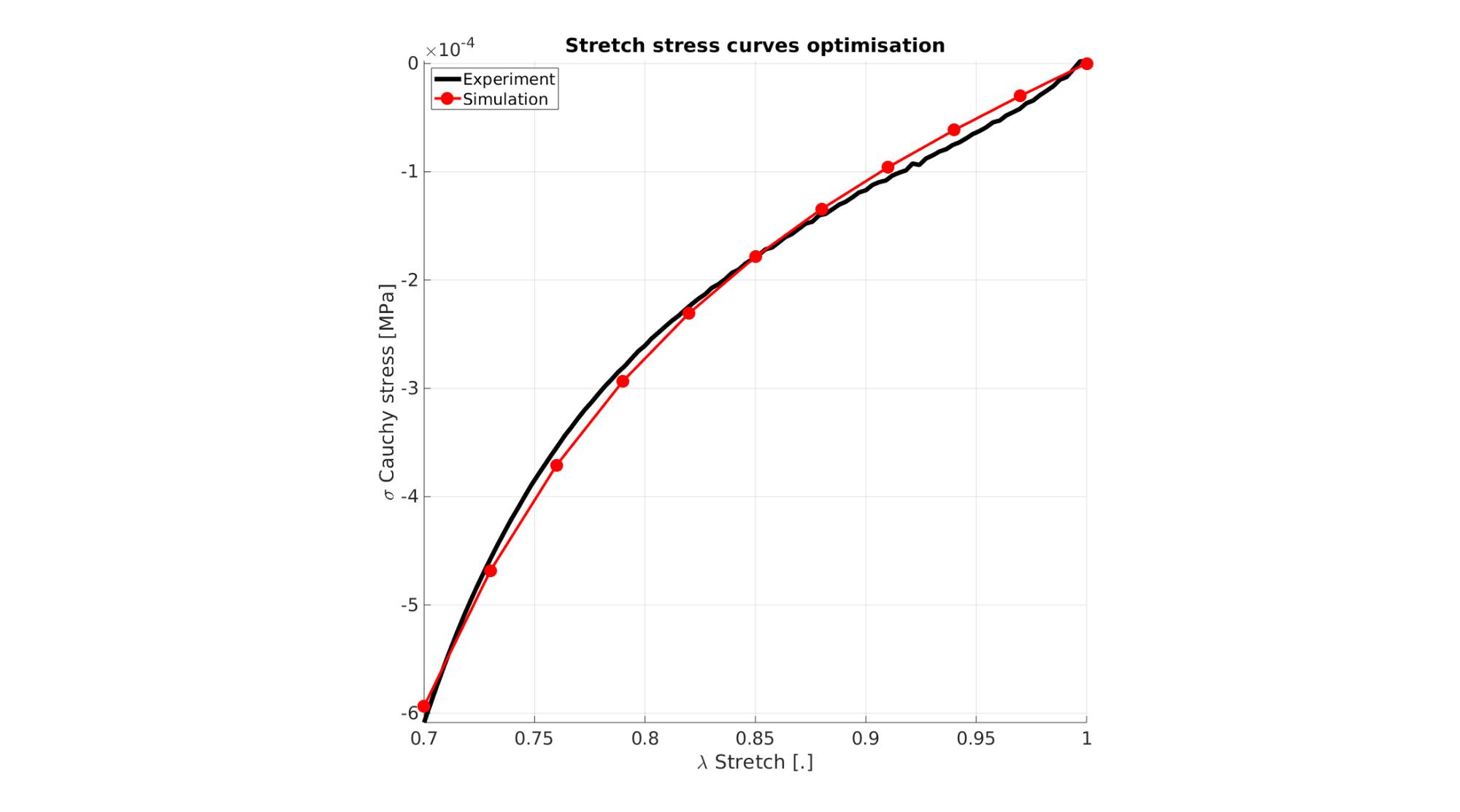
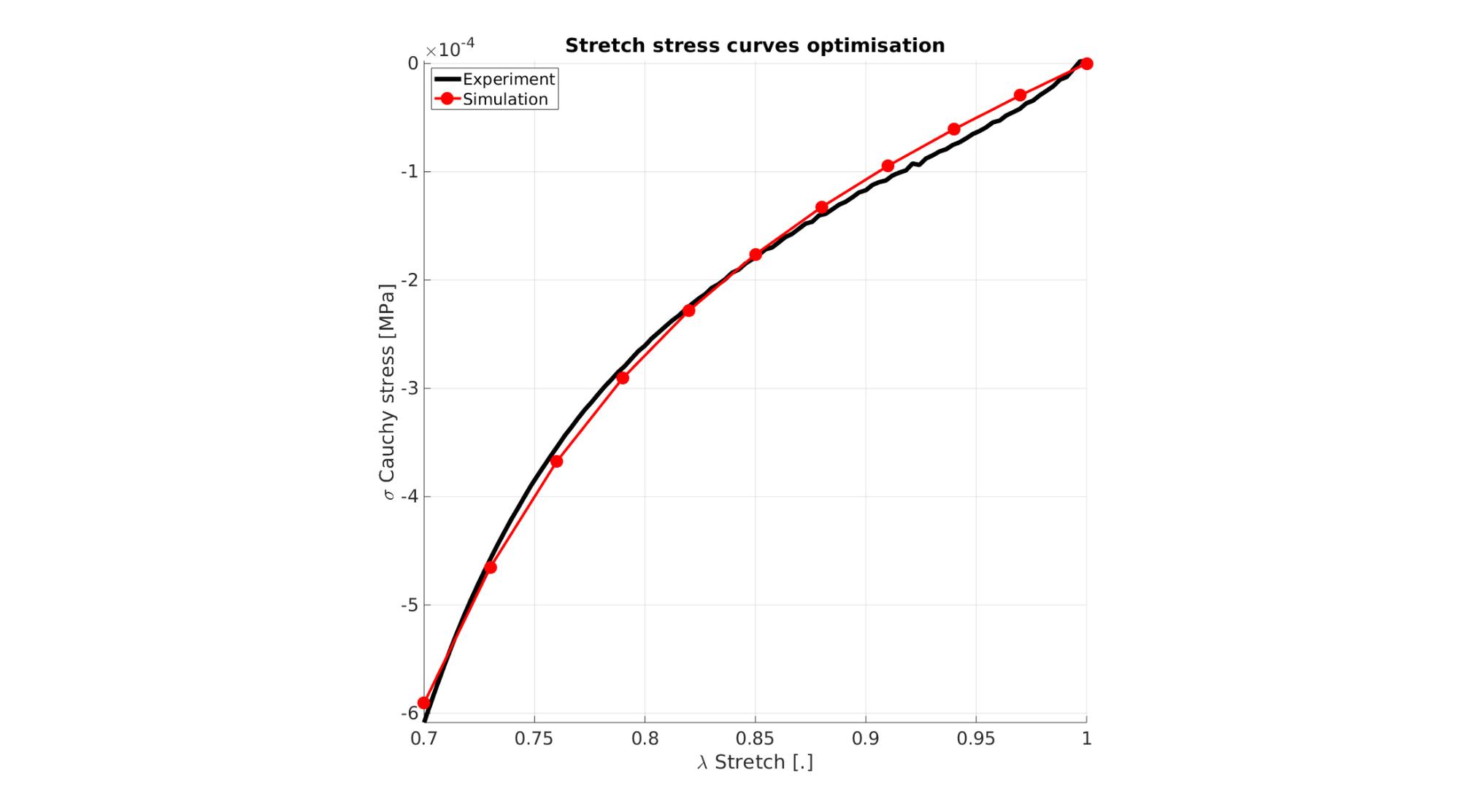
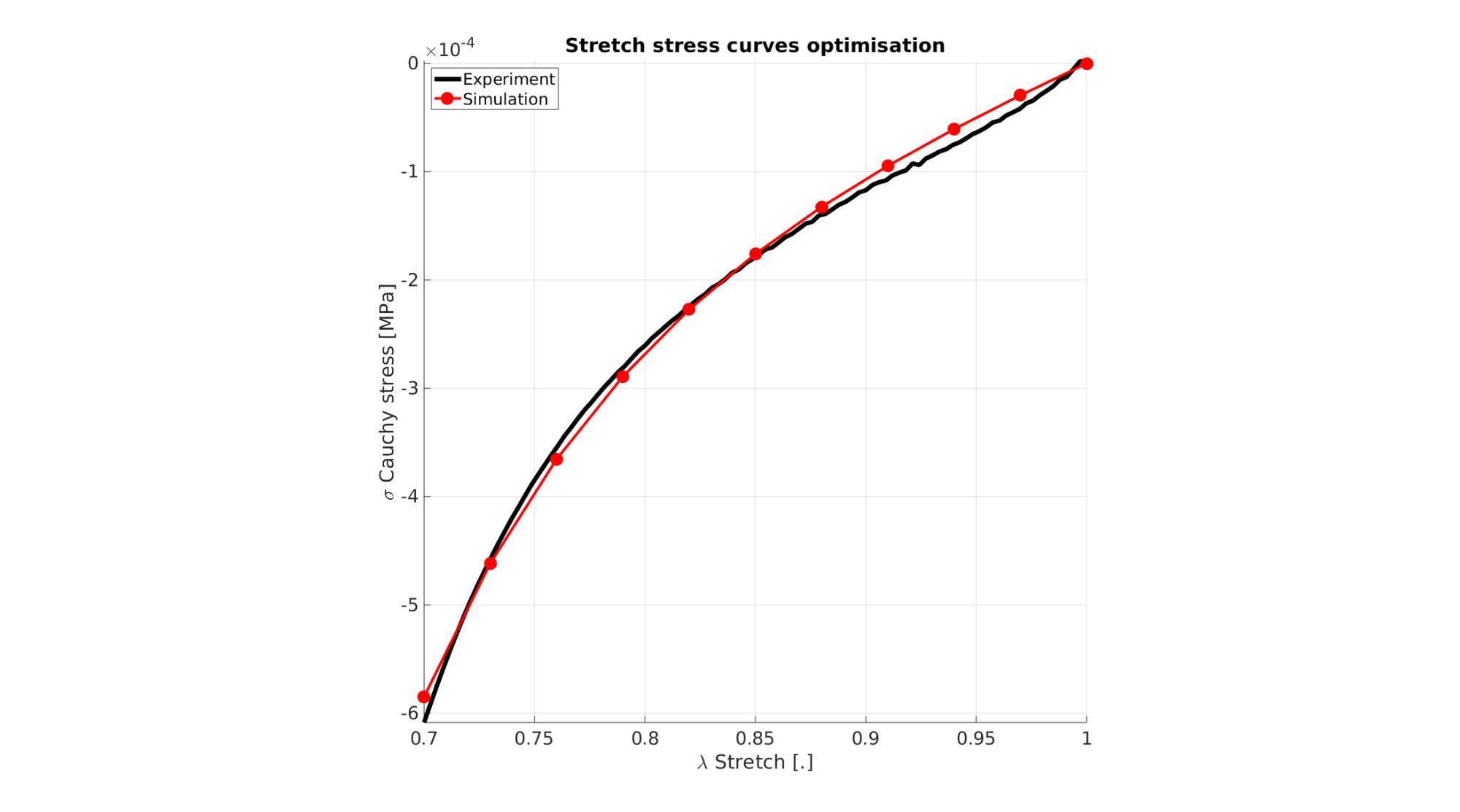
Visualize stress-stretch curve

    cFigure; hold on;
    title('Stretch stress curves optimisation','FontSize',fontSize);
    xlabel('\lambda Stretch [.]','FontSize',fontSize); ylabel('\sigma Cauchy stress [MPa]','FontSize',fontSize); zlabel('Z','FontSize',fontSize); hold on;

    Hn(1)=plot(stretch_exp,stress_cauchy_exp,'k-','lineWidth',lineWidth);
    view(2); axis tight;  grid on; axis square; axis manual;
    Hn(2)=plot(stretch_sim,stress_cauchy_sim,'r.-','lineWidth',lineWidth2,'markerSize',markerSize2);
    legend(Hn,{'Experiment','Simulation'},'Location','northwest');
    set(gca,'FontSize',fontSize);
    drawnow;

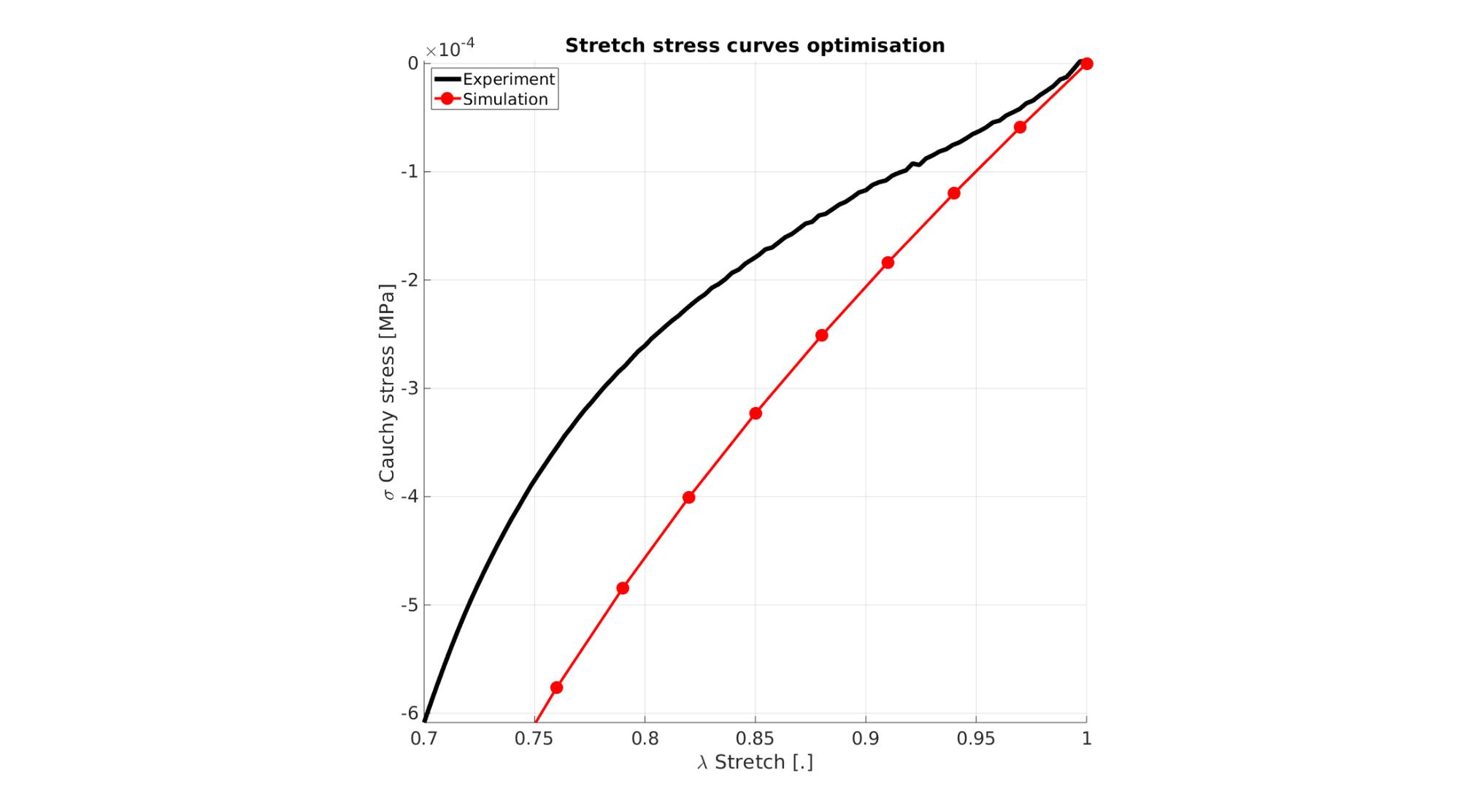
end

Create structures for optimization

% Material structure
mat_struct.id=1; %Material id
mat_struct.par_names={'c1','m1','c2','m2','k'}; %Parameter names
mat_struct.par_values={c1_ini m1_ini c1_ini -m1_ini k_ini}; %Parameter values

febioAnalysis.disp_on=0;
febioAnalysis.disp_log_on=0;

%What should be known to the objective function:
objectiveStruct.h=Hn(2);
objectiveStruct.stretch_exp=stretch_exp;
objectiveStruct.stress_cauchy_exp=stress_cauchy_exp;
objectiveStruct.febioAnalysis=febioAnalysis;
objectiveStruct.febio_spec=febio_spec;
objectiveStruct.febioFebFileName=febioFebFileName;
objectiveStruct.mat_struct=mat_struct;
objectiveStruct.k_factor=k_factor;
objectiveStruct.parNormFactors=P; %This will normalize the parameters to ones(size(P))
objectiveStruct.Pb_struct.xx_c=P; %Parameter constraining centre
objectiveStruct.Pb_struct.xxlim=[P(1)/100 P(1)*100;...
                                 2        50      ]; %Parameter bounds

%Optimisation settings
maxNumberIterations=100; %Maximum number of optimization iterations
maxNumberFunctionEvaluations=maxNumberIterations*10; %Maximum number of function evaluations, N.B. multiple evaluations are used per iteration
functionTolerance=1e-6; %Tolerance on objective function value
parameterTolerance=1e-6; %Tolerance on parameter variation
displayTypeIterations='iter';

objectiveStruct.method=2;

%File names of output files
output_names.stress=fullfile(savePath,febioLogFileName_stress);
output_names.stretch=fullfile(savePath,febioLogFileName_stretch);
objectiveStruct.run_output_names=output_names;

start optimization

Pn=P./objectiveStruct.parNormFactors;

switch objectiveStruct.method
    case 1 %fminsearch and Nelder-Mead
        OPT_options=optimset('fminsearch'); % 'Nelder-Mead simplex direct search'
        OPT_options = optimset(OPT_options,'MaxFunEvals',maxNumberFunctionEvaluations,...
            'MaxIter',maxNumberIterations,...
            'TolFun',functionTolerance,...
            'TolX',parameterTolerance,...
            'Display',displayTypeIterations,...
            'FinDiffRelStep',1e-2,...
            'DiffMaxChange',0.5);
        [Pn_opt,OPT_out.fval,OPT_out.exitflag,OPT_out.output]= fminsearch(@(Pn) objectiveFunctionIFEA(Pn,objectiveStruct),Pn,OPT_options);
    case 2 %lsqnonlin and Levenberg-Marquardt
        OPT_options = optimoptions(@lsqnonlin,'Algorithm','levenberg-marquardt');
        OPT_options = optimoptions(OPT_options,'MaxFunEvals',maxNumberFunctionEvaluations,...
            'MaxIter',maxNumberIterations,...
            'TolFun',functionTolerance,...
            'TolX',parameterTolerance,...
            'Display',displayTypeIterations,...
            'FinDiffRelStep',1e-2,...
            'DiffMaxChange',0.5);
        [Pn_opt,OPT_out.resnorm,OPT_out.residual]= lsqnonlin(@(Pn) objectiveFunctionIFEA(Pn,objectiveStruct),Pn,[],[],OPT_options);
end

[Fopt,OPT_stats_out]=objectiveFunctionIFEA(Pn_opt,objectiveStruct);

Unnormalize and constrain parameters

P_opt=Pn_opt.*objectiveStruct.parNormFactors; %Scale back, undo normalization

%Constraining parameters
for q=1:1:numel(P)
    [P(q)]=boxconstrain(P(q),objectiveStruct.Pb_struct.xxlim(q,1),objectiveStruct.Pb_struct.xxlim(q,2),objectiveStruct.Pb_struct.xx_c(q));
end

disp_text=sprintf('%6.16e,',P_opt); disp_text=disp_text(1:end-1);
disp(['P_opt=',disp_text]);

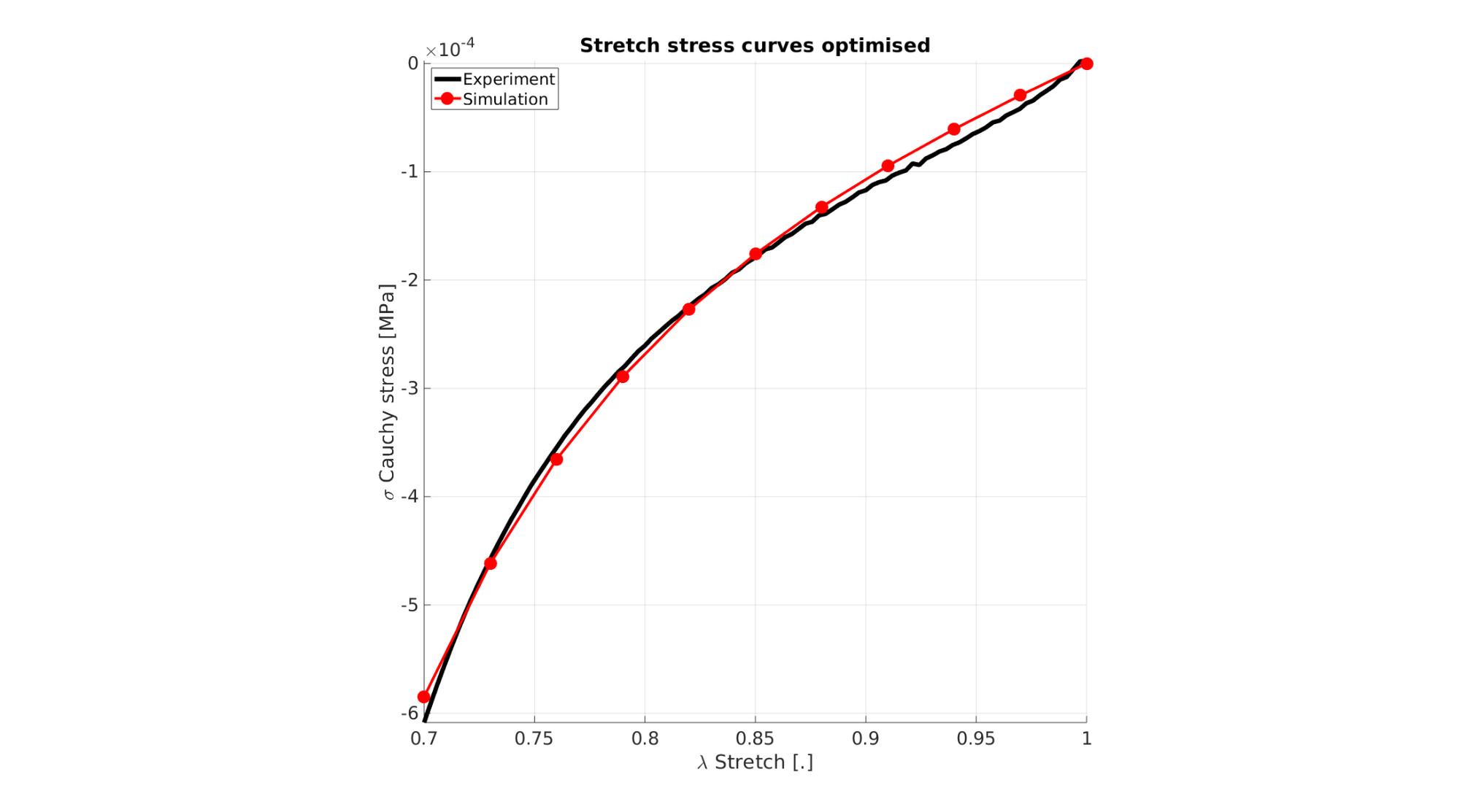
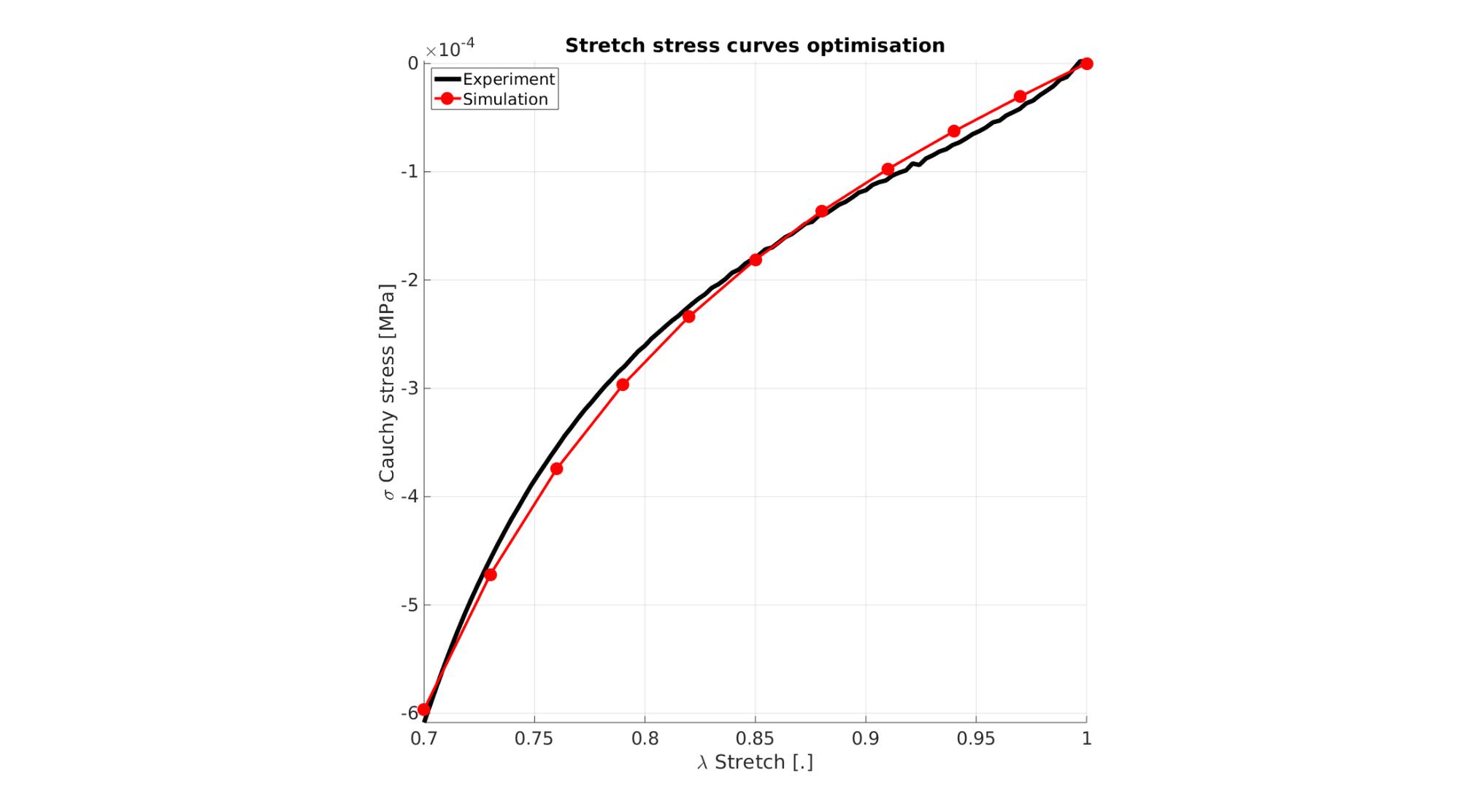
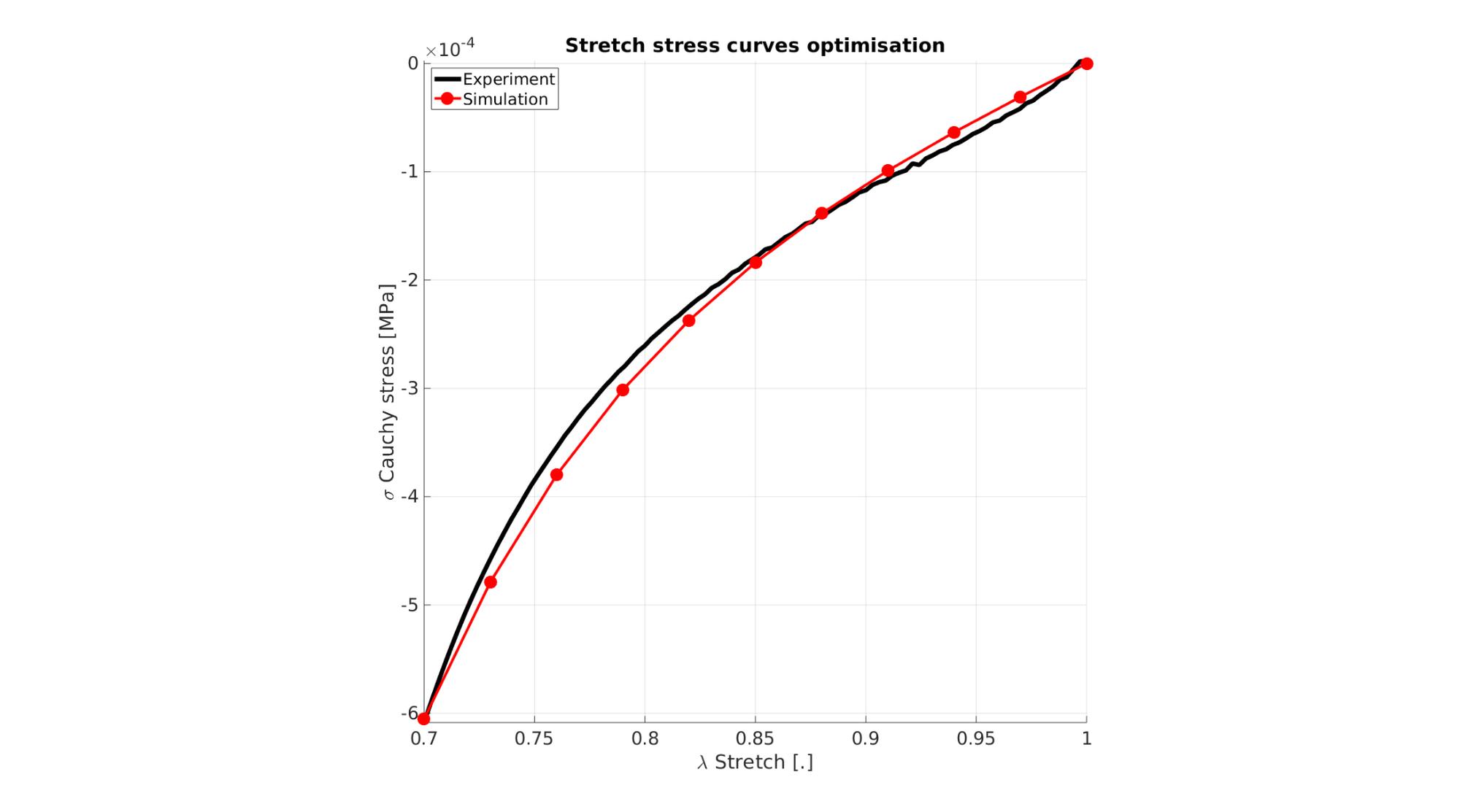
P_opt=2.8909803100416506e-04,6.0065568084440022e+00

cFigure; hold on;
title('Stretch stress curves optimised','FontSize',fontSize);
xlabel('\lambda Stretch [.]','FontSize',fontSize); ylabel('\sigma Cauchy stress [MPa]','FontSize',fontSize); zlabel('Z','FontSize',fontSize); hold on;

Hn(1)=plot(stretch_exp,stress_cauchy_exp,'k-','lineWidth',lineWidth);
Hn(2)=plot(OPT_stats_out.stretch_sim,OPT_stats_out.stress_cauchy_sim,'r.-','lineWidth',lineWidth2,'markerSize',markerSize2);

legend(Hn,{'Experiment','Simulation'},'Location','northwest');
view(2); axis tight;  grid on; axis square; axis manual;
set(gca,'FontSize',fontSize);
drawnow;

function [Fopt,OPT_stats_out]=objectiveFunctionIFEA(Pn,objectiveStruct)

febioFebFileName=objectiveStruct.febioFebFileName;
febio_spec=objectiveStruct.febio_spec;

Unnormalize and constrain parameters

P=Pn.*objectiveStruct.parNormFactors; %Scale back, undo normalization
P_in=P; %Proposed P

%Constraining parameters
for q=1:1:numel(P)
    [P(q)]=boxconstrain(P(q),objectiveStruct.Pb_struct.xxlim(q,1),objectiveStruct.Pb_struct.xxlim(q,2),objectiveStruct.Pb_struct.xx_c(q));
end

Setting material parameters

%Acces material parameters
mat_struct=objectiveStruct.mat_struct;
mat_struct.par_values={P(1) P(2) P(1) -P(2) P(1)*objectiveStruct.k_factor};

disp('SETTING MATERIAL PARAMETERS...');
disp(['Proposed (norm.): ',sprintf(repmat('%6.16e ',[1,numel(Pn)]),Pn)]);
disp(['Proposed        : ',sprintf(repmat('%6.16e ',[1,numel(P_in)]),P_in)]);
disp(['Set (constr.)   : ',sprintf(repmat('%6.16e ',[1,numel(P)]),P)]);

%Assign material parameters
matId=mat_struct.id;
for q=1:1:numel(mat_struct.par_names)
    parNameNow=mat_struct.par_names{q};
    parValuesNow=mat_struct.par_values{q};
    febio_spec.Material.material{matId}.(parNameNow)=mat2strIntDouble(parValuesNow);
end
febioStruct2xml(febio_spec,febioFebFileName); %Exporting to file and domNode

disp('Done')

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 1.0000000000000000e+00 1.0000000000000000e+00 
Proposed        : 6.4464428523599996e-04 3.0000000000000000e+00 
Set (constr.)   : 6.4464428523599996e-04 3.0000000000000000e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 1.0100000000000000e+00 1.0000000000000000e+00 
Proposed        : 6.5109072808836000e-04 3.0000000000000000e+00 
Set (constr.)   : 6.5109072806643559e-04 3.0000000000000000e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 1.0000000000000000e+00 1.0100000000000000e+00 
Proposed        : 6.4464428523599996e-04 3.0300000000000002e+00 
Set (constr.)   : 6.4464428523599996e-04 3.0299999959257593e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.9938198939115996e-01 9.9990320940432753e-01 
Proposed        : 6.4424588822879596e-04 2.9997096282129827e+00 
Set (constr.)   : 6.4424588828054666e-04 2.9997096282211437e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 1.0093819893911600e+00 9.9990320940432753e-01 
Proposed        : 6.5069233108115600e-04 2.9997096282129827e+00 
Set (constr.)   : 6.5069233106305037e-04 2.9997096282211437e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.9938198939115996e-01 1.0099032094043274e+00 
Proposed        : 6.4424588822879596e-04 3.0297096282129825e+00 
Set (constr.)   : 6.4424588828054666e-04 3.0297096242559047e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.9330917958767229e-01 9.9895423478641654e-01 
Proposed        : 6.4033108609365256e-04 2.9968627043592497e+00 
Set (constr.)   : 6.4033115176239178e-04 2.9968627146522828e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 1.0033091795876723e+00 9.9895423478641654e-01 
Proposed        : 6.4677752894601250e-04 2.9968627043592497e+00 
Set (constr.)   : 6.4677752894521799e-04 2.9968627146522828e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.9330917958767229e-01 1.0089542347864164e+00 
Proposed        : 6.4033108609365256e-04 3.0268627043592495e+00 
Set (constr.)   : 6.4033115176239178e-04 3.0268627014342071e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.4169235373033311e-01 9.9106873757067060e-01 
Proposed        : 6.0705659428269708e-04 2.9732062127120118e+00 
Set (constr.)   : 6.0709999559465256e-04 2.9732126226874609e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.5169235373033312e-01 9.9106873757067060e-01 
Proposed        : 6.1350303713505702e-04 2.9732062127120118e+00 
Set (constr.)   : 6.1352772950092440e-04 2.9732126226874609e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 9.4169235373033311e-01 1.0010687375706706e+00 
Proposed        : 6.0705659428269708e-04 3.0032062127120120e+00 
Set (constr.)   : 6.0709999559465256e-04 3.0032062127070387e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 7.5376621666648802e-01 9.6884319671767283e-01 
Proposed        : 4.8591108397801205e-04 2.9065295901530184e+00 
Set (constr.)   : 4.8910525924269696e-04 2.9068008504117495e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 7.6376621666648803e-01 9.6884319671767283e-01 
Proposed        : 4.9235752683037210e-04 2.9065295901530184e+00 
Set (constr.)   : 4.9518355627003021e-04 2.9068008504117495e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 7.5376621666648802e-01 9.7884319671767284e-01 
Proposed        : 4.8591108397801205e-04 2.9365295901530186e+00 
Set (constr.)   : 4.8910525924269696e-04 2.9366146830695263e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 6.3381239446636395e-01 1.0097124215516684e+00 
Proposed        : 4.0858353800448684e-04 3.0291372646550050e+00 
Set (constr.)   : 4.1879091583189810e-04 3.0291372609222518e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 6.4381239446636396e-01 1.0097124215516684e+00 
Proposed        : 4.1502998085684683e-04 3.0291372646550050e+00 
Set (constr.)   : 4.2445004430345711e-04 3.0291372609222518e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 6.3381239446636395e-01 1.0198095457671852e+00 
Proposed        : 4.0858353800448684e-04 3.0594286373015556e+00 
Set (constr.)   : 4.1879091583189810e-04 3.0594286056299511e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 5.7633128093430652e-01 1.3718081475429156e+00 
Proposed        : 3.7152866665704433e-04 4.1154244426287470e+00 
Set (constr.)   : 3.8706433944149288e-04 4.1152150768633575e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 5.8633128093430653e-01 1.3718081475429156e+00 
Proposed        : 3.7797510950940432e-04 4.1154244426287470e+00 
Set (constr.)   : 3.9248258017452137e-04 4.1152150768633575e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 5.7633128093430652e-01 1.3855262290183448e+00 
Proposed        : 3.7152866665704433e-04 4.1565786870550347e+00 
Set (constr.)   : 3.8706433944149288e-04 4.1563452856846315e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.7018609794163391e-01 1.9767061026089379e+00 
Proposed        : 3.0310278103548848e-04 5.9301183078268132e+00 
Set (constr.)   : 3.3236147055638095e-04 5.9263280927469886e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.8018609794163392e-01 1.9767061026089379e+00 
Proposed        : 3.0954922388784847e-04 5.9301183078268132e+00 
Set (constr.)   : 3.3728860231407951e-04 5.9263280927469886e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.7018609794163391e-01 1.9964731636350272e+00 
Proposed        : 3.0310278103548848e-04 5.9894194909050817e+00 
Set (constr.)   : 3.3236147055638095e-04 5.9853947177135014e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.4898899892561145e-01 2.0006046437868812e+00 
Proposed        : 2.8943819229122796e-04 6.0018139313606440e+00 
Set (constr.)   : 3.2207795762981631e-04 5.9977389436561479e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.5898899892561146e-01 2.0006046437868812e+00 
Proposed        : 2.9588463514358795e-04 6.0018139313606440e+00 
Set (constr.)   : 3.2690203990156600e-04 5.9977389436561479e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.4898899892561145e-01 2.0206106902247498e+00 
Proposed        : 2.8943819229122796e-04 6.0618320706742495e+00 
Set (constr.)   : 3.2207795762981631e-04 6.0575080224553499e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.4846132607586559e-01 2.0021856028146674e+00 
Proposed        : 2.8909803100416506e-04 6.0065568084440022e+00 
Set (constr.)   : 3.2182476307718294e-04 6.0024624958101400e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.5846132607586559e-01 2.0021856028146674e+00 
Proposed        : 2.9554447385652511e-04 6.0065568084440022e+00 
Set (constr.)   : 3.2664626526004271e-04 6.0024624958101400e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.4846132607586559e-01 2.0222074588428143e+00 
Proposed        : 2.8909803100416506e-04 6.0666223765284428e+00 
Set (constr.)   : 3.2182476307718294e-04 6.0622780243797134e+00 
Done

SETTING MATERIAL PARAMETERS...
Proposed (norm.): 4.4846132607586559e-01 2.0021856028146674e+00 
Proposed        : 2.8909803100416506e-04 6.0065568084440022e+00 
Set (constr.)   : 3.2182476307718294e-04 6.0024624958101400e+00 
Done

START FEBio

[runFlag]=runMonitorFEBio(objectiveStruct.febioAnalysis);

%pause(0.1);

stretch_exp=objectiveStruct.stretch_exp;
stress_cauchy_exp=objectiveStruct.stress_cauchy_exp;

if runFlag==1

    % Importing element stress from a log file
    [~, E_stress_mat,~]=importFEBio_logfile(objectiveStruct.run_output_names.stress,0,1);

    % Importing element stress from a log file
    [~, E_stretch_mat,~]=importFEBio_logfile(objectiveStruct.run_output_names.stretch,0,1);

    stretch_sim=squeeze(mean(E_stretch_mat,1)); % Stretch U_z
    stress_cauchy_sim=squeeze(mean(E_stress_mat,1)); %Cauchy stress sigma_z

    if ~isempty(objectiveStruct.h)
        objectiveStruct.h.XData=stretch_sim;
        objectiveStruct.h.YData=stress_cauchy_sim;
        drawnow;
    end

    %Interpolate experiment onto simulated points
    stress_cauchy_sim_exp = interp1(stretch_sim,stress_cauchy_sim,stretch_exp,'pchip');

    %Derive Fopt
    stressDev=stress_cauchy_exp-stress_cauchy_sim_exp;

    switch objectiveStruct.method
        case 1
            Fopt=sum((stressDev).^2); %Sum of squared differences
        case 2
            Fopt=stressDev(:);%(stressDev).^2; %Squared differences
    end

    OPT_stats_out.stress_cauchy_sim=stress_cauchy_sim;
    OPT_stats_out.stretch_sim=stretch_sim;
    OPT_stats_out.stressDev=stressDev;
    OPT_stats_out.Fopt=Fopt;

else %Output NaN
    switch objectiveStruct.method
        case 1
            Fopt=NaN;
        case 2
            Fopt=NaN(size(stress_cauchy_exp)); %Squared differences
    end
    OPT_stats_out=[];
end

end

                                        First-order                     Norm of 
 Iteration  Func-count      Resnorm      optimality       Lambda           step
     0           3      2.30665e-06        6.19e-06         0.01
     1           6      2.29882e-06        6.18e-06        0.001    0.000625544
     2           9      2.22262e-06        6.07e-06       0.0001     0.00614651
     3          12      1.63058e-06        5.14e-06        1e-05      0.0522157
     4          15      3.08386e-07        1.85e-06        1e-06       0.189236
     5          18      7.90879e-08        1.61e-07        1e-07       0.126725
     6          21      4.21922e-08         7.9e-08        1e-08        0.36663
     7          24      1.30793e-08        2.59e-07        1e-09        0.61414
     8          27      8.91615e-09        2.73e-09        1e-10      0.0319446
     9          30      8.91549e-09        5.99e-12        1e-11     0.00166669

Local minimum found.

Optimization completed because the size of the gradient is less than
1e-4 times the value of the function tolerance.

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

DEMO_febio_0042_inverse_FEA_cube_uniaxial

Contents

Keywords

Control parameters

SIMULATE EXPERIMENTAL DATA

CREATING MESHED BOX

DEFINE BC's

Defining the FEBio input structure

Quick viewing of the FEBio input file structure

Exporting the FEBio input file

Running the FEBio analysis

Import FEBio results

Create structures for optimization

start optimization

Unnormalize and constrain parameters

Unnormalize and constrain parameters

Setting material parameters

START FEBio