DEMO_imx_levelset_surface_compare

Below is a demonstration for:

Contents

Keywords

clear; close all; clc;

Plot settings

fontSize=10;
faceAlpha1=1;
faceAlpha2=0.3;
plotColors=gjet(4);

defaultFolder = fileparts(fileparts(mfilename('fullpath'))); %Set main folder
pathName=fullfile(defaultFolder,'data','imseg');
loadNames={'imseg_torus_1','imseg_torus_2'};

Simulate image

Defining an example triangulated surface model

% Defining a deformed and rotated torus shape
r=1; %Sphere radius
rc=2; %Central radius
nr=16;
nc=30;
ptype='tri';
[F,V]=patchTorus(r,nr,rc,nc,ptype);
[THETA,RHO] = cart2pol(V(:,1),V(:,2));

Setting control parameters

% Defining the full set of possible control parameters
voxelSize=0.15; % The output image voxel size.
imOrigin=min(V,[],1)-4*voxelSize;
imMax=max(V,[],1)+4*voxelSize;
imSiz=round((imMax-imOrigin)/voxelSize);
imSiz=imSiz([2 1 3]); %Image size (x, y corresponds to j,i in image coordinates, hence the permutation)

% Using |triSurf2Im| function to convert patch data to image data
[M,G,bwLabels]=triSurf2Im(F,V,voxelSize,imOrigin,imSiz);

%calucalte coordinate in image system
Vt=V-imOrigin(ones(size(V,1),1),:);

Plotting the results

hf1=cFigure;
subplot(1,2,1);
title('Closed triangulated surface','FontSize',fontSize);
xlabel('X','FontSize',fontSize);ylabel('Y','FontSize',fontSize); zlabel('Z','FontSize',fontSize);
hold on;
patch('Faces',F,'Vertices',V,'FaceColor','g','EdgeColor','k','FaceAlpha',faceAlpha1);
camlight('headlight'); lighting flat;
axis equal; view(3); axis tight;  grid on;  set(gca,'FontSize',fontSize);

subplot(1,2,2);
title('Boundary, intertior and exterior image','FontSize',fontSize);
xlabel('X','FontSize',fontSize);ylabel('Y','FontSize',fontSize); zlabel('Z','FontSize',fontSize);
hold on;

patch('Faces',F,'Vertices',V,'FaceColor','g','EdgeColor','none','FaceAlpha',faceAlpha2);
L_plot=false(size(M));
L_plot(:,:,round(size(M,3)/2))=1;
[Fm,Vm,Cm]=ind2patch(L_plot,double(M),'sk');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
patch('Faces',Fm,'Vertices',Vm,'FaceColor','flat','CData',Cm,'EdgeColor','k','FaceAlpha',faceAlpha1);

L_plot=false(size(M));L_plot(round(size(M,1)/2),:,:)=1;
[Fm,Vm,Cm]=ind2patch(L_plot,M,'si');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
patch('Faces',Fm,'Vertices',Vm,'FaceColor','flat','CData',Cm,'EdgeColor','k','FaceAlpha',faceAlpha1);

L_plot=false(size(M));L_plot(:,round(size(M,2)/2),:)=1;
[Fm,Vm,Cm]=ind2patch(L_plot,M,'sj');
[Vm(:,1),Vm(:,2),Vm(:,3)]=im2cart(Vm(:,2),Vm(:,1),Vm(:,3),voxelSize*ones(1,3));
Vm=Vm+imOrigin(ones(size(Vm,1),1),:);
patch('Faces',Fm,'Vertices',Vm,'FaceColor','flat','CData',Cm,'EdgeColor','k','FaceAlpha',faceAlpha1);

colormap(gray(3)); caxis([0 2]);
hc=colorbar;
set(hc,'YTick',[1/3 1 5/3]);
set(hc,'YTickLabel',{'Exterior','Boundary','Intertior'});
axis equal; view(3); axis tight;  grid on;  set(gca,'FontSize',fontSize);
drawnow;

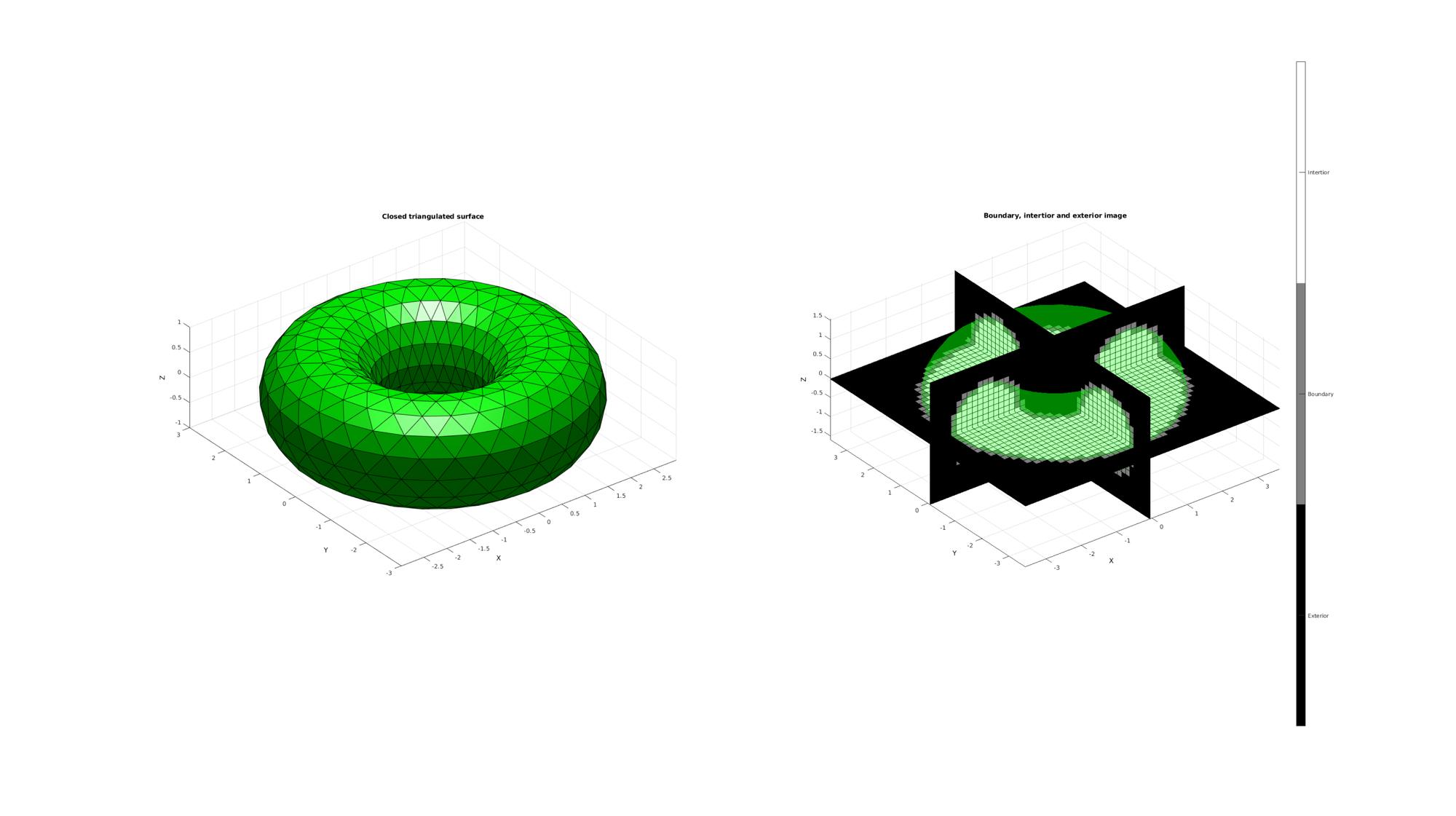
Start contour selection using imx

Use imx to draw contours for tissue boundaries of interest.

v=voxelSize*ones(1,3); %Voxel size
hf=imx(M,v); %Start image contour analysis
drawnow;

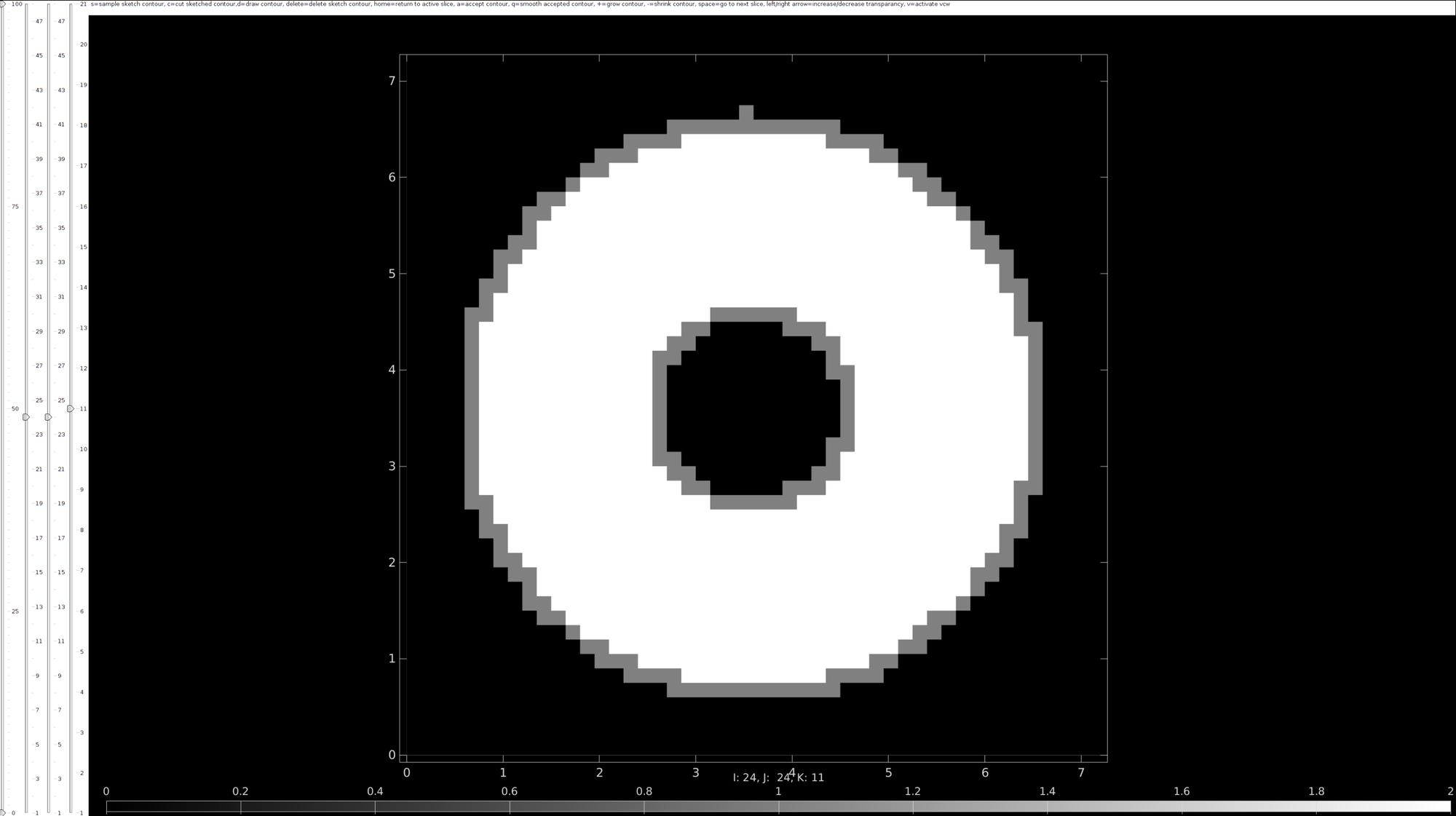
Upload previously completed contours

You can upload complete contours by using the load button. Try to load in imseg_torus_1.mat or imseg_torus_2.mat from...GIBBON/data/imseg/

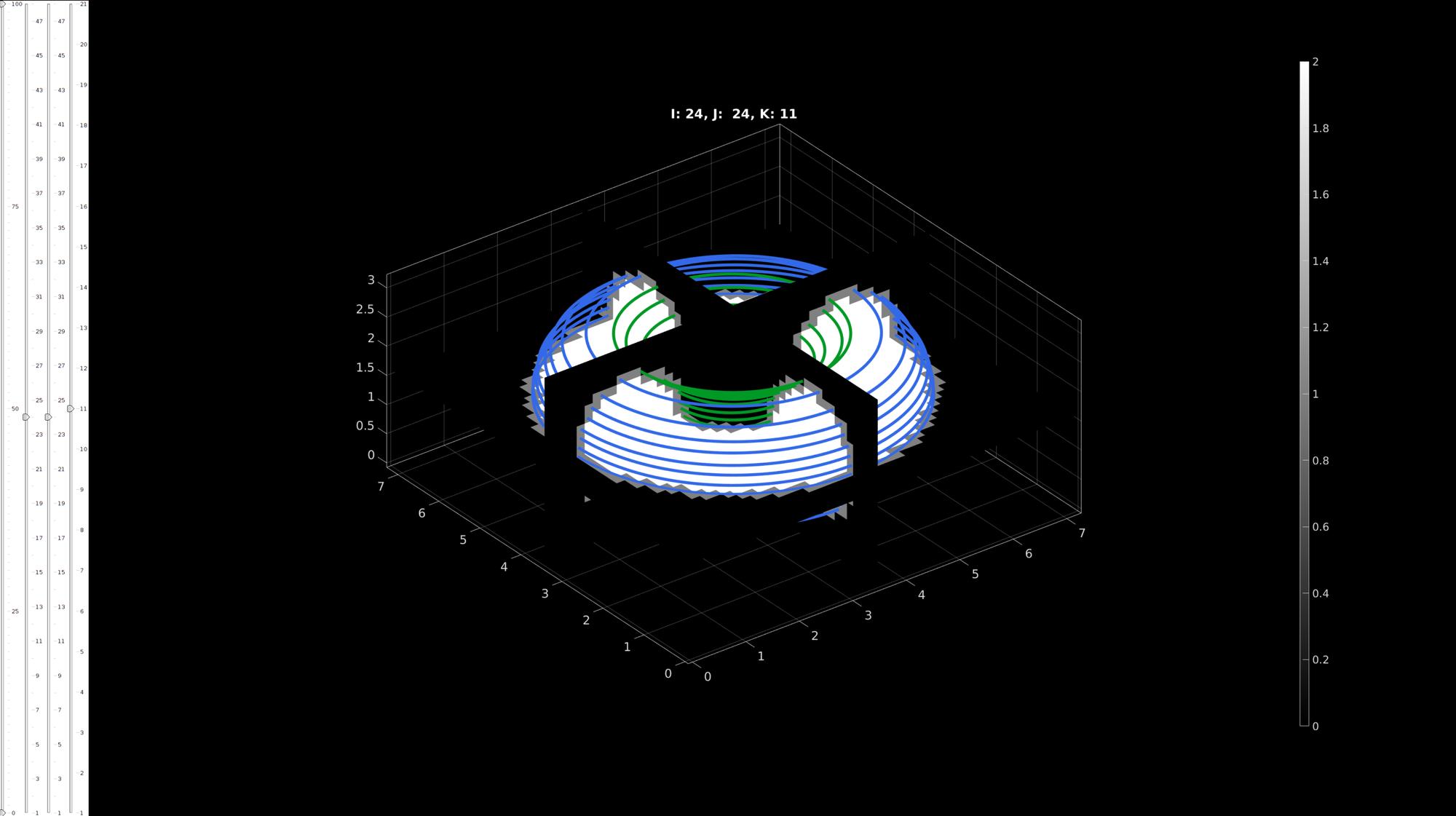
Example converting completed contours into levelset function

The surface should exist at the level 0

% Start simple slice viewer
sv3(M,v);
drawnow;

numContours=numel(loadNames);
numSlices=size(M,3);

levelSetType=3;
logicIn=repmat(M,1,1,1,2);
logicOn=repmat(M,1,1,1,2);
for q=1:1:2
    loadName=fullfile(pathName,loadNames{q});
    load(loadName);
    Vcs=saveStruct.ContourSet;
    [L_in,L_on]=contour2logic(M,v,Vcs);
    logicIn(:,:,:,q)=L_in;
    logicOn(:,:,:,q)=L_on;
    for qSlice=1:1:numSlices
        numSubContours=numel(Vcs{qSlice});
        for qSub=1:1:numSubContours
            Vd=Vcs{qSlice}{qSub}; %Current contour
            if ~isempty(Vd)
                hp=plotV(Vd,'w-');
                hp.Color=plotColors(q,:);
                hp.LineWidth=5;
            end
        end
    end

end
logicInside=(logicIn(:,:,:,1) | logicOn(:,:,:,1)) & ~logicIn(:,:,:,2);

[K]=logic2levelset(logicInside,v);

Visualize levelset

vizStruct.colormap=warmcold(250); %colormap
vizStruct.clim=[-max(abs(K(:))) max(abs(K(:)))]; %color limits

hf1q=sv3(K,v,vizStruct);

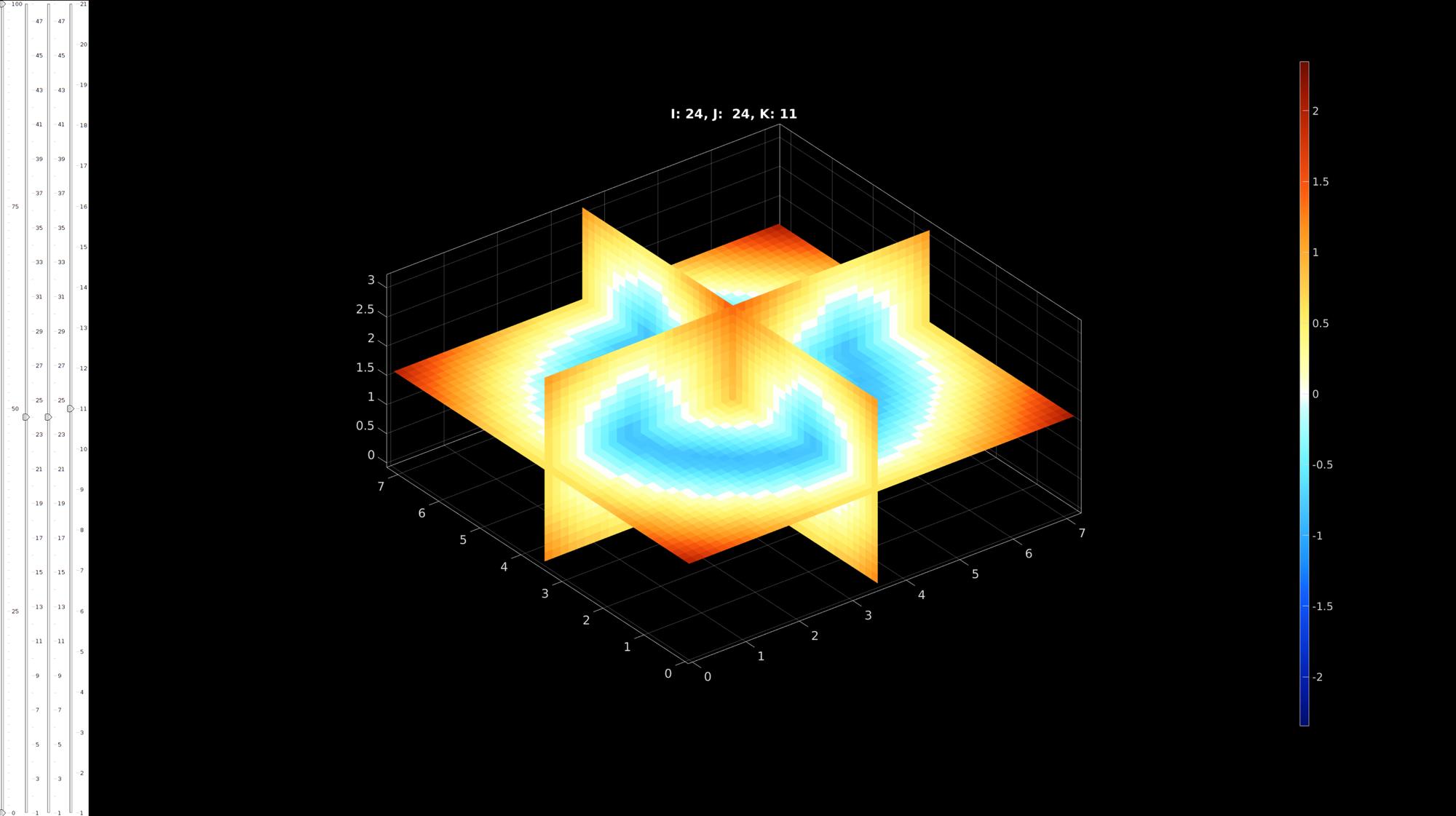
Convert levelset function to a surface

controlPar.contourLevel=0;
controlPar.voxelSize=v;
controlPar.nSub=[1 1 1];
controlPar.capOpt=1;

[Fi,Vi]=levelset2isosurface(K,controlPar);
Fi=fliplr(Fi); %Invert orientation

Surface improvement and smoothing

%Remove tri-connected parts
[Fi,Vi]=triSurfRemoveThreeConnect(Fi,Vi,[]);

%Smoothen
cParSmooth.Method='HC';
cParSmooth.Alpha=0.1;
cParSmooth.Beta=0.5;
cParSmooth.n=10;
[Vi]=patchSmooth(Fi,Vi,[],cParSmooth);

Compare to theoretical original

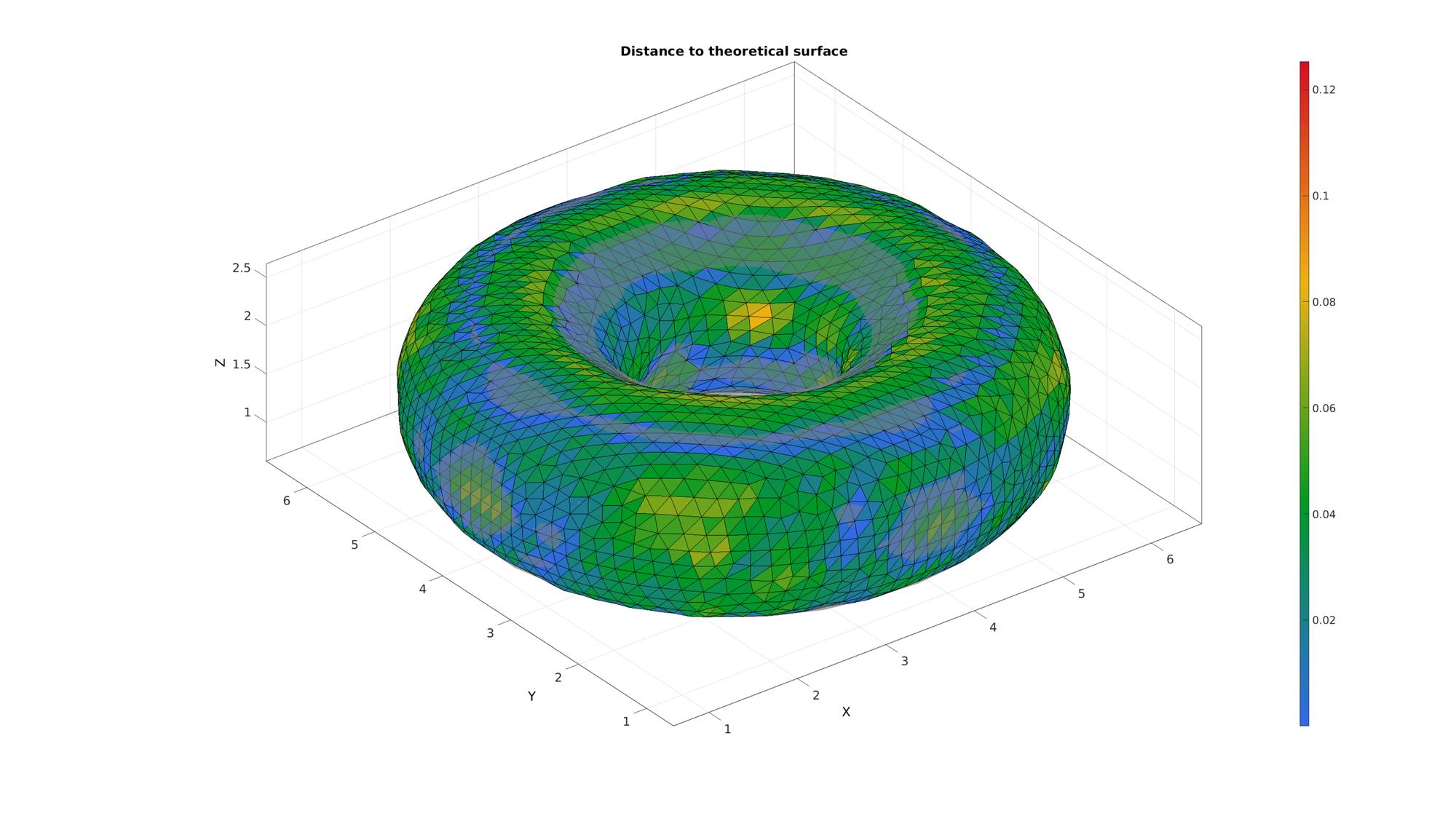
Compare by computing distance with ray-tracing method.

[Di]=triSurfSetDist(Fi,Vi,F,Vt,'dist-ray');

Visualize distance measure

cFigure;
title('Distance to theoretical surface');
hold on;
gpatch(F,Vt,0.5*ones(1,3),'none',0.5);
hp=gpatch(Fi,Vi,Di,'k',1);
caxis([min(Di(:)) max(Di(:))]);
colormap(gjet(250)); colorbar;
axisGeom;
drawnow

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a