FFT_derivative

Below is a demonstration of the features of the FFT_derivative function

Syntax
Description
Examples
FFT derivatives of evenly spaced vector data
Using extrapolation to suppress edge effects
FFT derivatives of multi-dimensional data

clear; close all; clc;

Syntax

[dY,fft_dY]=FFT_derivative(dt,Y,dimDer,derOrder,numPad);

Description

This function uses the Fourier transform method to compute the derivative of order derOrder for the input data Y, allong direction dimDer. The array X

Examples

Plot settings

fontSize=20;
lineWidth=5;

FFT derivatives of evenly spaced vector data

Create example data

n=50; %Number of samples
x=linspace(0,3*pi,n); %x-vector
y=sin(x); %y-vector
dy=cos(x); %True derivative for comparison

Use FFT_derivative to compute the derivative

dimDer=2; %Direction for derivative
derOrder=1; %Order of derivative
dt=x(2)-x(1);
dy_fft=FFT_derivative(dt,y,dimDer,derOrder);

Visualize data

cFigure;
subplot(1,2,1); hold on;
title('Input curve');
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
plot(x,y,'k.-','lineWidth',lineWidth,'MarkerSize',25);
axis square; axis tight; grid on; box on;
set(gca,'FontSize',fontSize);

subplot(1,2,2); hold on;
title('derivatives');
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
hp1=plot(x,dy,'k.-','lineWidth',lineWidth,'MarkerSize',25);
hp2=plot(x,dy_fft,'r.-','lineWidth',lineWidth/2,'MarkerSize',25);
axis square; axis tight; grid on; box on;
set(gca,'FontSize',fontSize);
legend([hp1 hp2],{'True derivative','FFT based derivative'});

drawnow;

%

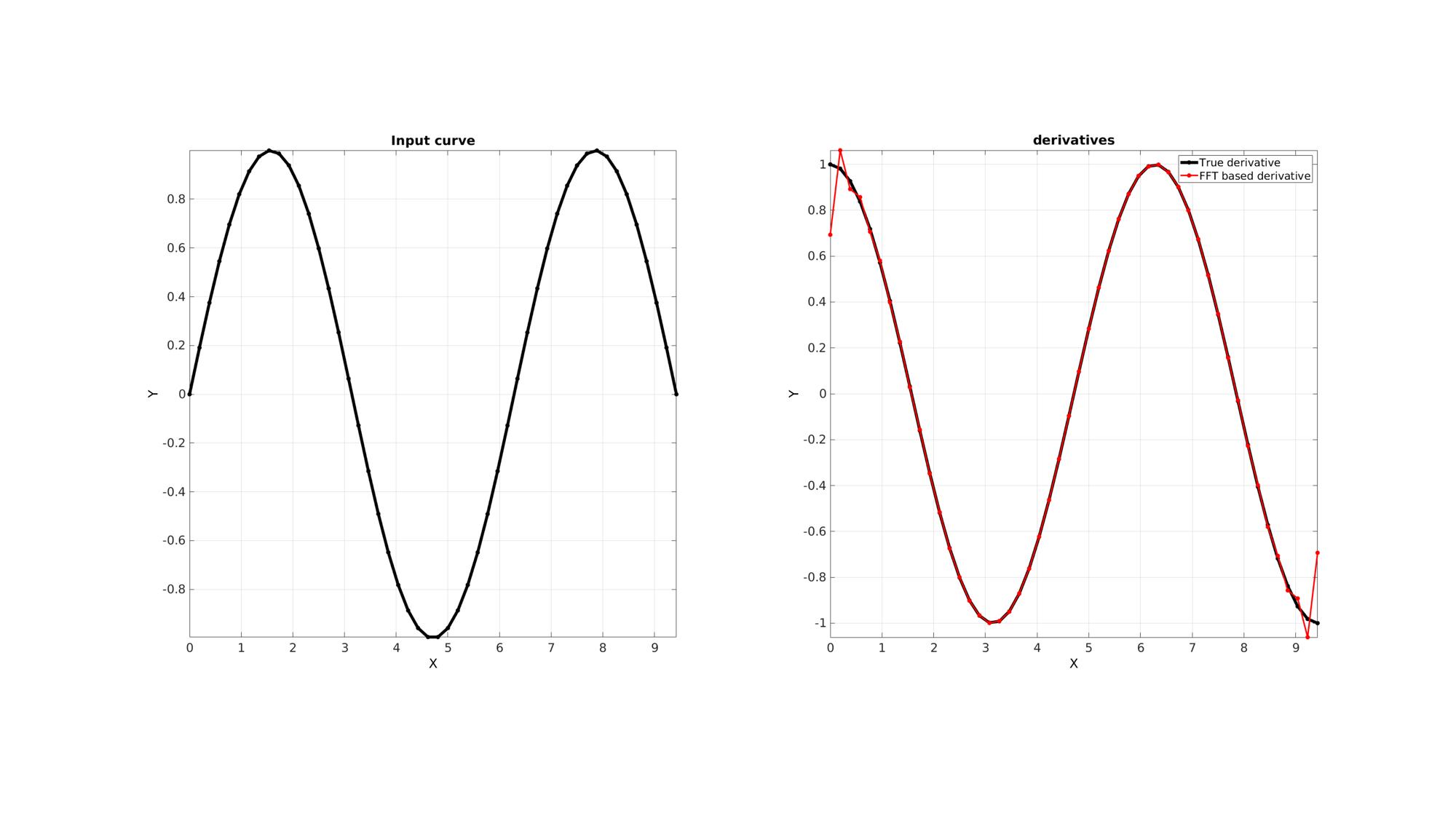
Using extrapolation to suppress edge effects

Use FFT_derivative to compute the derivative

dimDer=2; %Direction for derivative
derOrder=1; %Order of derivative
numPad=ceil(size(y,dimDer)/4);
dt=x(2)-x(1);
dy_fft=FFT_derivative(dt,y,dimDer,derOrder,numPad);

Visualize data

cFigure;
subplot(1,2,1); hold on;
title('Input curve');
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
plot(x,y,'k.-','lineWidth',lineWidth,'MarkerSize',25);
axis square; axis tight; grid on; box on;
set(gca,'FontSize',fontSize);

subplot(1,2,2); hold on;
title('derivatives');
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
hp1=plot(x,dy,'k.-','lineWidth',lineWidth,'MarkerSize',25);
hp2=plot(x,dy_fft,'r.-','lineWidth',lineWidth/2,'MarkerSize',25);
axis square; axis tight; grid on; box on;
set(gca,'FontSize',fontSize);
legend([hp1 hp2],{'True derivative','FFT based derivative'});

drawnow;

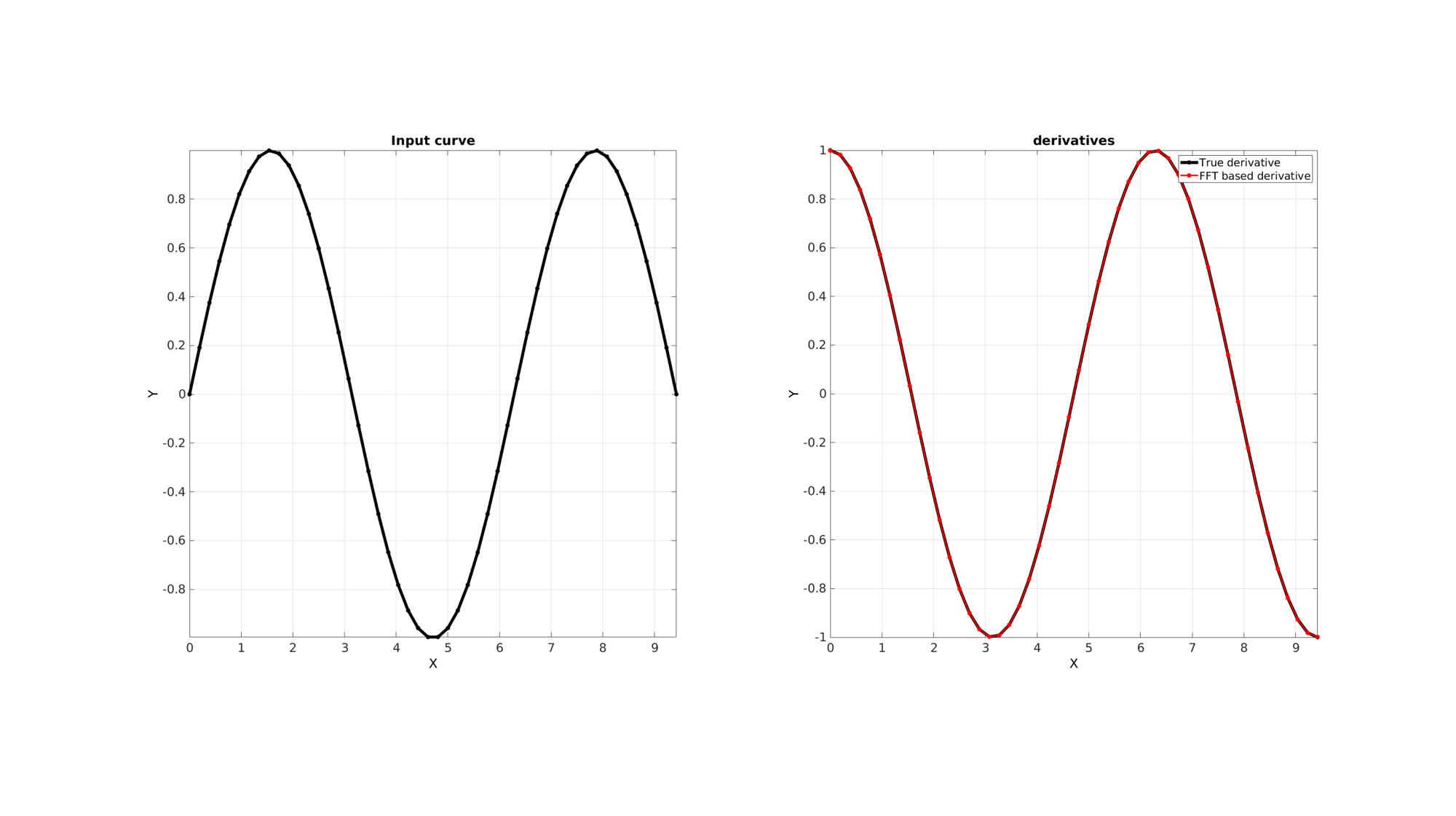
FFT derivatives of multi-dimensional data

Create example data array

% Expand x-data from previous example into array
nRep=25;
X=x(ones(nRep,1),:); %X-data array
Y=sin(X); %Y-data array
DY=cos(X); %True derivative

dimDer=2;
derOrder=1;
numPad=ceil(size(y,dimDer)/4);
dt=x(2)-x(1);
dY_fft=FFT_derivative(dt,Y,dimDer,derOrder,numPad);

cFigure;
subplot(2,2,1); hold on;
title('Input data ')
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
imagesc(Y);
axis square; axis tight; grid on;
set(gca,'FontSize',fontSize);
colorbar;

subplot(2,2,2); hold on;
title('True derivative')
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
imagesc(DY);
axis square; axis tight; grid on;
set(gca,'FontSize',fontSize);
colorbar;

subplot(2,2,3); hold on;
title('FFT based derivative')
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
imagesc(dY_fft);
axis square; axis tight; grid on;
set(gca,'FontSize',fontSize);
colorbar;

subplot(2,2,4); hold on;
title('Difference')
xlabel('X','FontSize',fontSize); ylabel('Y','FontSize',fontSize);
imagesc(DY-dY_fft);
axis square; axis tight; grid on;
set(gca,'FontSize',fontSize);
colorbar;

drawnow;

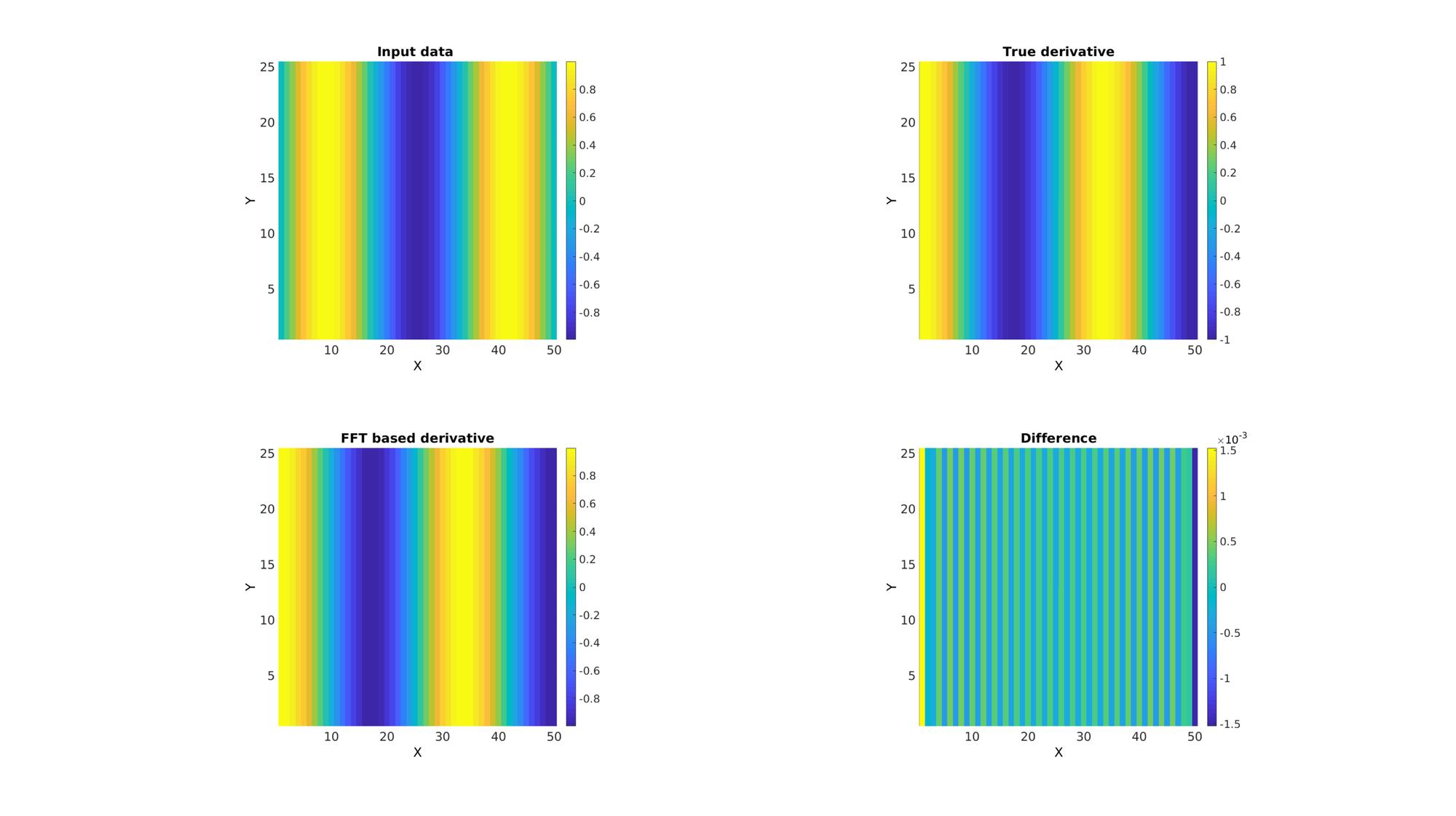
GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.