diamondLattice

Below is a demonstration of the features of the diamondLattice function

Syntax
Description
Examples
Create diamond lattice
Build refined and smooth triangulated surface mesh

clear; close all; clc;

Syntax

[Ep,Et,VT]=diamondLattice(sampleSize,nRepeat,strutThickness,latticePhaseType);

Description

This functions creates element/patch data for the diamond lattice

Plotting settings

fontSize=15;
faceAlpha1=0.8;
faceAlpha2=1;
edgeColor=0.25*ones(1,3);
edgeWidth=1.5;
markerSize=25;
markerSize2=10;
cMap=gjet(4);

Examples

%Latticeparameters
nRepeat=3; %Number of repetitions of the lattice pattern
sampleSize=30;
nSubPenta=1;
strutThickness=2; %Set the strut thickness
latticePhaseType=1;  % 1 = "bubble" centred, 2 = vertex centred, 3 = nested

Create diamond lattice

[Ep,Et,VT]=diamondLattice(sampleSize,nRepeat,strutThickness,latticePhaseType);
[Ep,VT]=subPenta(Ep,VT,nSubPenta,3); %Sub-divide pentahedra

%Get element faces for visualization
Fp=element2patch(Ep,[],'penta6');
Ft=element2patch(Et,[],'tet4');
% strutThicknessCheck=mean(patchEdgeLengths(Fp{1},VT))

Visualization

cFigure;
subplot(1,2,1); hold on;
gpatch(Fp,VT,'bw','k',1);
gpatch(Ft,VT,'bw','k',1);
axisGeom; camlight headlight;

subplot(1,2,2); hold on;
hpl=gpatch(Fp,VT,'rw','r',0.5);
hpl(end+1)=gpatch(Ft,VT,'gw','g',0.5);
legend(hpl,{'Pentahedral triangles','Pentahedra quads','Tetrahedral triangles'});
axisGeom; camlight headlight;

drawnow;

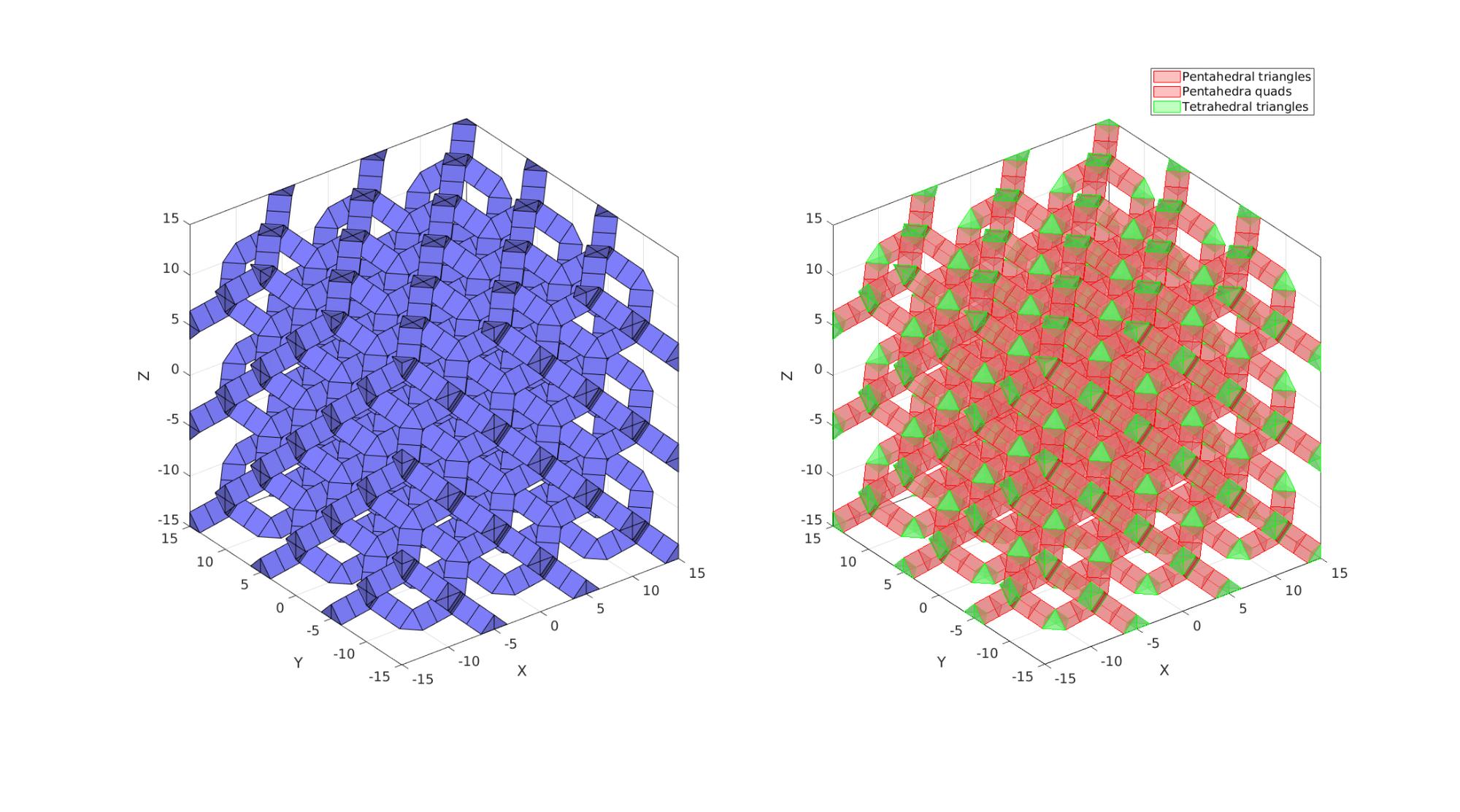
Build refined and smooth triangulated surface mesh

Fpt=[Fp{1}; Fp{2}(:,[1 2 3]);Fp{2}(:,[3 4 1])];
FT=[Fpt;Ft];
[FT,VT]=patchCleanUnused(FT,VT);

FTs=sort(FT,2);
[A_uni,ind1,ind2,Ac]=cunique(FTs,'rows');

[FT,VT]=patchCleanUnused(FT(Ac==1,:),VT);

CT=zeros(size(FT,1),1);
for q=1:1:3
    X=VT(:,q);
    XF=X(FT);
    CT(all(XF>=(max(X(:))-eps(max(X(:)))),2))=max(CT(:))+1;
    CT(all(XF <(min(X(:))+eps(min(X(:)))),2))=max(CT(:))+1;
end

% %%
% % Visualization
%
% cFigure; hold on;
% gpatch(FT,VT,CT,'k',1);
% axisGeom; camlight headlight;
% colormap gjet; icolorbar;
% drawnow;

Refine using Loop-subdivision

n=2;
logicConstrain=(CT>0); %Logic for faces to subdivide linearly
indConstrain=find(logicConstrain);
indNotConstrain=find(~logicConstrain);

[Fs1,Vs1,Cs1]=subTriLoop(FT(logicConstrain,:),VT,n);
faceBoundaryMarker_sub1=CT(indConstrain(Cs1)); %Get boundary markers for refined mesh

[Fs2,Vs2,Cs2]=subTriLoop(FT(~logicConstrain,:),VT,n);
faceBoundaryMarker_sub2=CT(indNotConstrain(Cs2)); %Get boundary markers for refined mesh

[Fs,Vs,Cs]=joinElementSets({Fs1,Fs2},{Vs1,Vs2},{faceBoundaryMarker_sub1,faceBoundaryMarker_sub2});

[Fs,Vs]=patchCleanUnused(Fs,Vs);
[Fs,Vs]=mergeVertices(Fs,Vs);

%Fix boundary faces
dir=[1 1 2 2 3 3];
for q=1:1:6
    ind=unique(FT(CT==q,:));
    ind_s=unique(Fs(Cs==q,:));
    Vs(ind_s,dir(q))=mean(VT(ind,dir(q)));
end

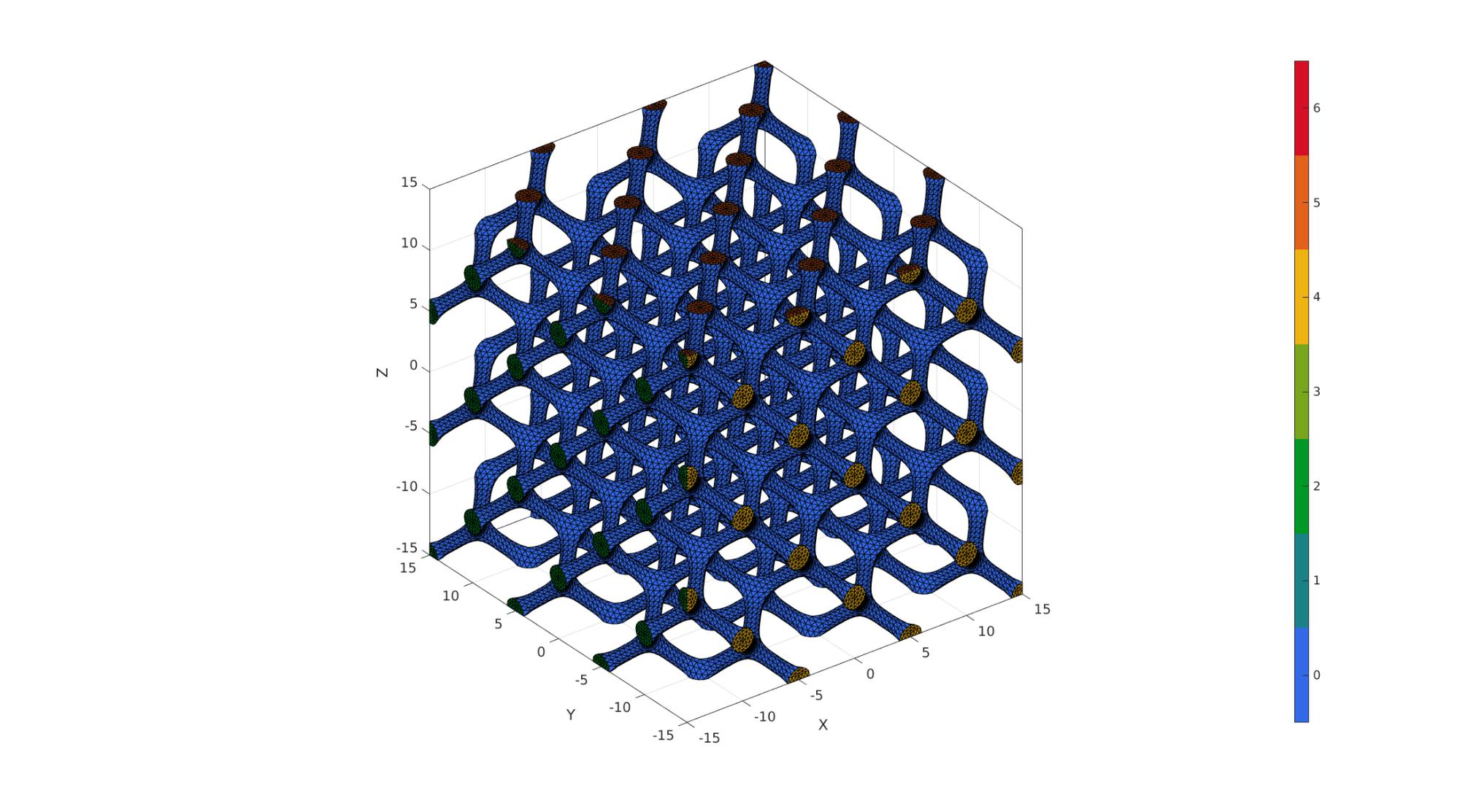
Visualization

cFigure; hold on;
gpatch(Fs,Vs,Cs,'k',1);
axisGeom; camlight headlight;
colormap gjet; icolorbar;
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.