HELP_ellipsoidFit_centered

Below is a demonstration of the features of the ellipsoidFit_centered function

Contents

Syntax

[M,ellipStretch,R,MU]=ellipsoidFit_centered(X,MU);

Description

The ellipsoidFit_centered function fits an ellipsoid to data when the ellipsoid centre is known. If the centre is not provided the mean of the input point set will be assumed to be the centre.

Examples

clear; close all; clc;

Plot settings

figColor='w';
figColorDef='white';
fontSize=11;

Example: Using ellipsoidFit_centered to fit an ellipsoid to a point cloud with known centre

Simulating an ellipsoid with known directions

% Ellipsoid axis stretch factors
ellipStretchTrue=[pi 2 0.5];
MU_true=[1 6 pi];

% Create ellipsoid patch data
[F,V,~]=geoSphere(3,1);
v=V(:,1);
FX=mean(v(F),2);
logicKeep=FX>0;
F=F(logicKeep,:);
indKeep=unique(F(:));
indFix=nan(size(V,1),1);
indFix(indKeep)=1:numel(indKeep);
V=V(indKeep,:);
F=indFix(F);
V=V.*ellipStretchTrue(ones(size(V,1),1),:);

%Create Euler angles to set directions
E=[0.25*pi 0.25*pi -0.25*pi];
[R_true,~]=euler2DCM(E); %The true directions for X, Y and Z axis
V=(R_true*V')'; %Rotate polyhedron

V=V+MU_true(ones(size(V,1),1),:); %Centre points around mean

%Add noise
n_std=0.2;  %Standard deviation
Vn=V+n_std.*randn(size(V));

This is the true axis system

R_true

R_true =

    0.5000    0.5000    0.7071
   -0.1464    0.8536   -0.5000
   -0.8536    0.1464    0.5000

These are the true stretch factors

ellipStretchTrue

ellipStretchTrue =

    3.1416    2.0000    0.5000

[M,ellipsStretchFit,R_fit,MU]=ellipsoidFit_centered(Vn,MU_true);

This is the fitted axis system. The system axes should be colinear with the true axes but can be oposite in direction.

R_fit=R_fit(1:3,1:3)

R_fit =

    0.4986   -0.5025   -0.7064
   -0.1336   -0.8497    0.5101
   -0.8565   -0.1599   -0.4908

These are the fitted stretch factors

ellipsStretchFit

ellipsStretchFit =

    3.0437    1.9999    0.6456

Building a fitted (clean) ellipsoid for visualization

%Create sphere
[F_fit,V_fit,~]=geoSphere(4,1);

%Transforming sphere to ellipsoid
V_fit_t=V_fit;
V_fit_t(:,end+1)=1;
V_fit_t=(M*V_fit_t')'; %Rotate polyhedron
V_fit=V_fit_t(:,1:end-1);

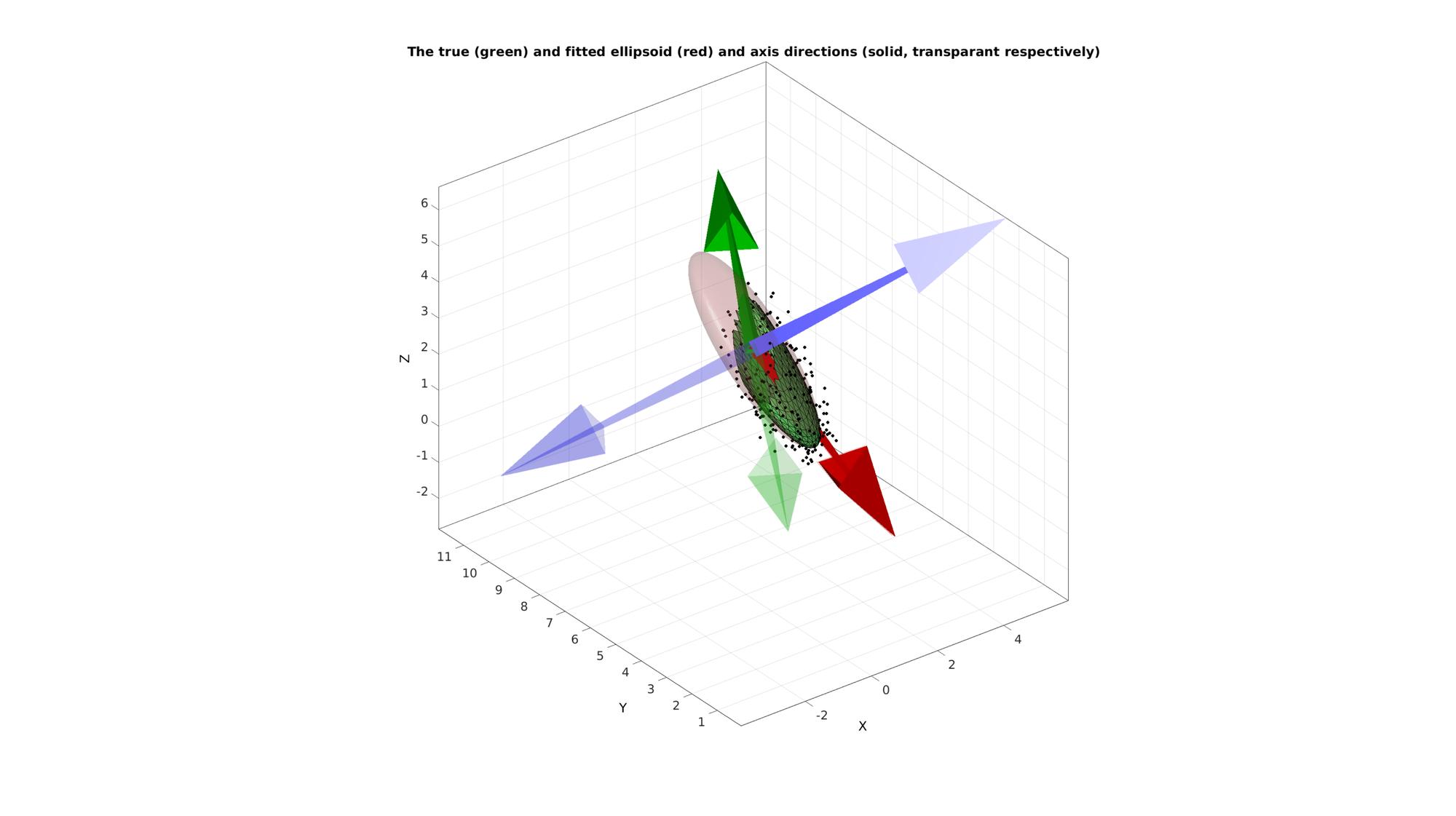
Visualizing results

cFigure; hold on;
title('The true (green) and fitted ellipsoid (red) and axis directions (solid, transparant respectively)','FontSize',fontSize);
plotV(Vn,'k.','MarkerSize',15);
gpatch(F,V,'gw','k',1);
gpatch(F_fit,V_fit,'rw','none',0.2);
quiverTriad(MU,R_fit,7,[],0.2);
quiverTriad(MU,R_true,7,[],1);
axisGeom;
camlight('headlight');
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a