fftnconv

Below is a demonstration of the features of the fftnconv function

Syntax
Description
Examples
Example 1: 1D convolution
Example 2: 2D convolution

clear; close all; clc;

Syntax

[MF]=fftnconv(M,F);

Description

DEPRICATED

Examples

Plot settings

lineWidth=3;

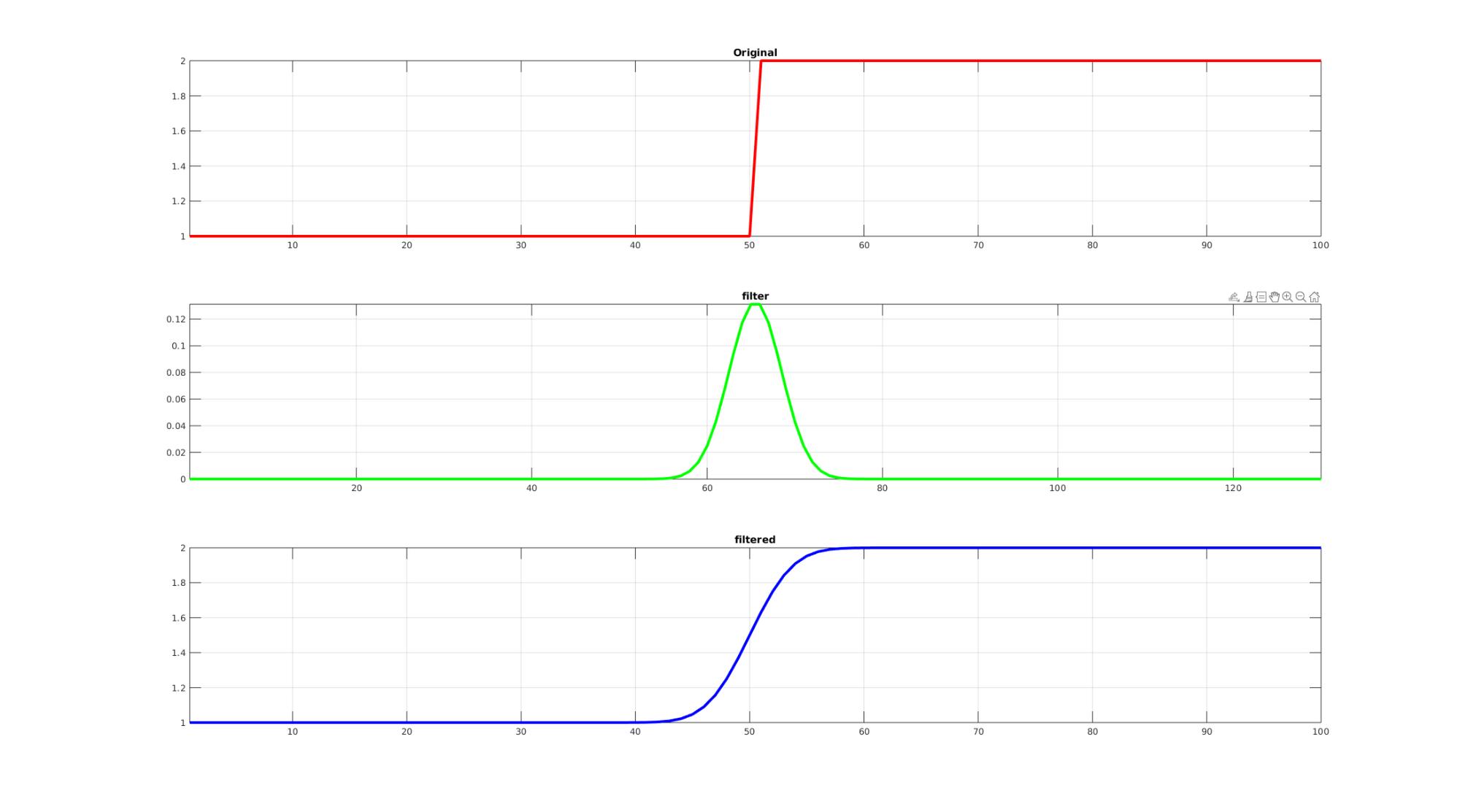
Example 1: 1D convolution

n=50;
m=[ones(1,n) 2*ones(1,n)];

kernelSigma=3;
padSize=kernelSigma*5;
padDim=2;

%Pad to avoid edge issues
[mp,indOriginal]=padLinDim(m,padSize,2);

%Compose filter
f=gauss_kernel(numel(mp),1,kernelSigma,'sigma');

%FFT based convolution
mfp=fftnconv(mp,f);

%Crop back to original size
siz=size(mp);
siz(padDim)=siz(padDim)-2*padSize;
mf=reshape(mfp(indOriginal),siz);

Visualization

cFigure;
subplot(3,1,1); hold on;
title('Original');
plot(m,'r-','LineWidth',lineWidth);
axis tight; grid on; box on;

subplot(3,1,2); hold on;
title('filter');
plot(f,'g-','LineWidth',lineWidth);
axis tight; grid on; box on;

subplot(3,1,3); hold on;
title('filtered');
plot(mf,'b-','LineWidth',lineWidth);
axis tight; grid on; box on;

drawnow;

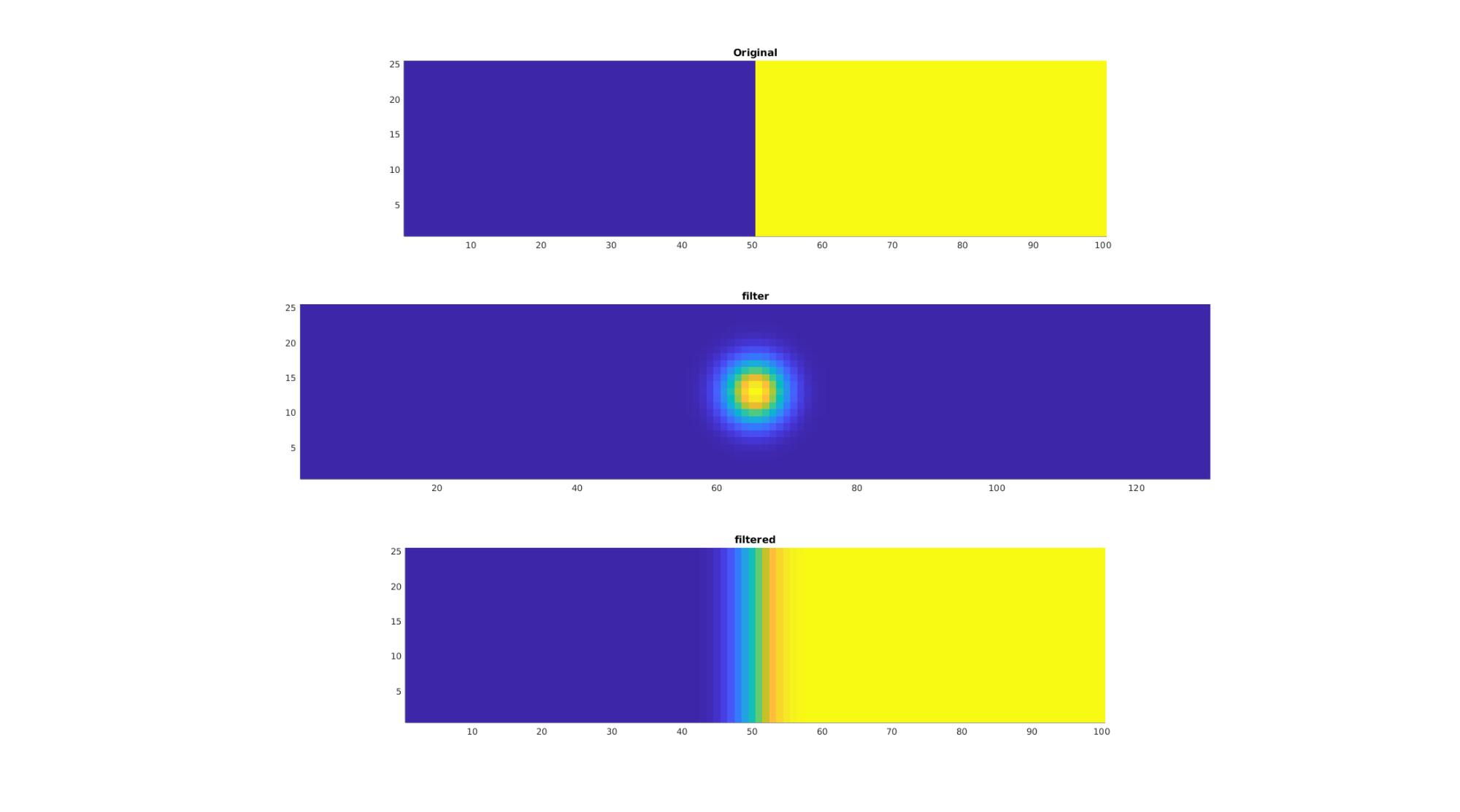
Example 2: 2D convolution

n=50;
m=[ones(25,n) 2*ones(25,n)];

kernelSigma=3;
padSize=kernelSigma*5;
padDim=2;

%Pad to avoid edge issues
[mp,indOriginal]=padLinDim(m,padSize,padDim);

%Compose filter
k=[size(mp,1) size(mp,2)];

[y,x] = meshgrid(linspace(-((k(2)-1)/2),((k(2)-1)/2),k(2)),linspace(-((k(1)-1)/2),((k(1)-1)/2),k(1)));
f=exp(-(x.^2 + y.^2)./(2*kernelSigma^2));

%FFT based convolution
mfp=fftnconv(mp,f);

%Crop back to original size
mf=reshape(mfp(indOriginal),size(m));

Visualization

cFigure;
subplot(3,1,1); hold on;
title('Original');
imagesc(m);
axis tight; axis equal;

subplot(3,1,2); hold on;
title('filter');
imagesc(f);
axis tight; axis equal;

subplot(3,1,3); hold on;
title('filtered');
imagesc(mf);
axis tight; axis equal;

drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.