patch_dual

Below is a demonstration of the features of the patch_dual function

Contents

Syntax

[Vd,Fd,Fds]=patch_dual(V,F);

Description

Computes the dual of the input tesselation defined by the vertices V and faces F.

Examples

clear; close all; clc;

Plot settings

fontSize=15;
plotColor1=0.25.*ones(1,3);
plotColor2=0.75.*ones(1,3);
edgeWidth=2;
markerSize=25;
cMap=gjet(250);

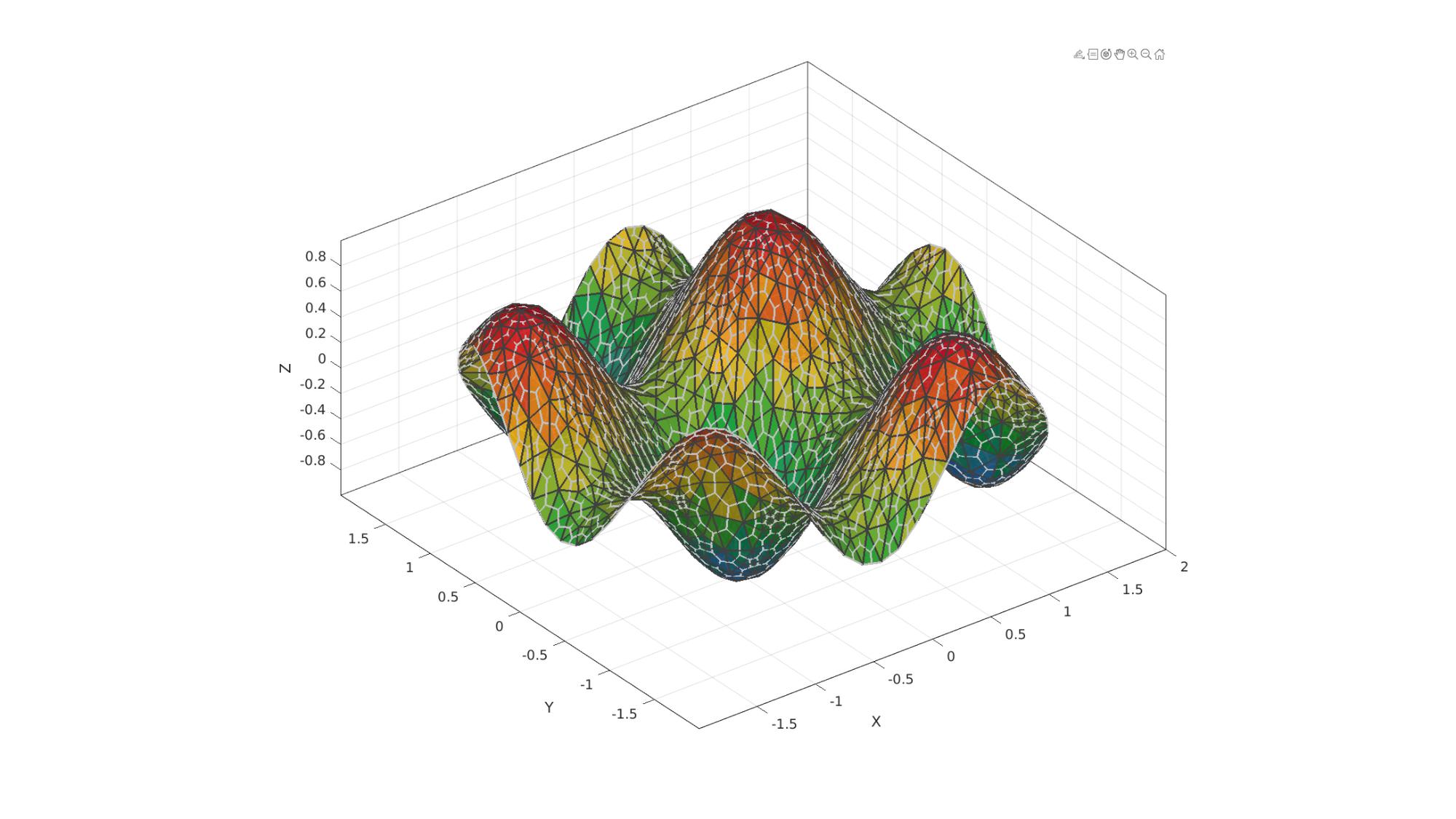
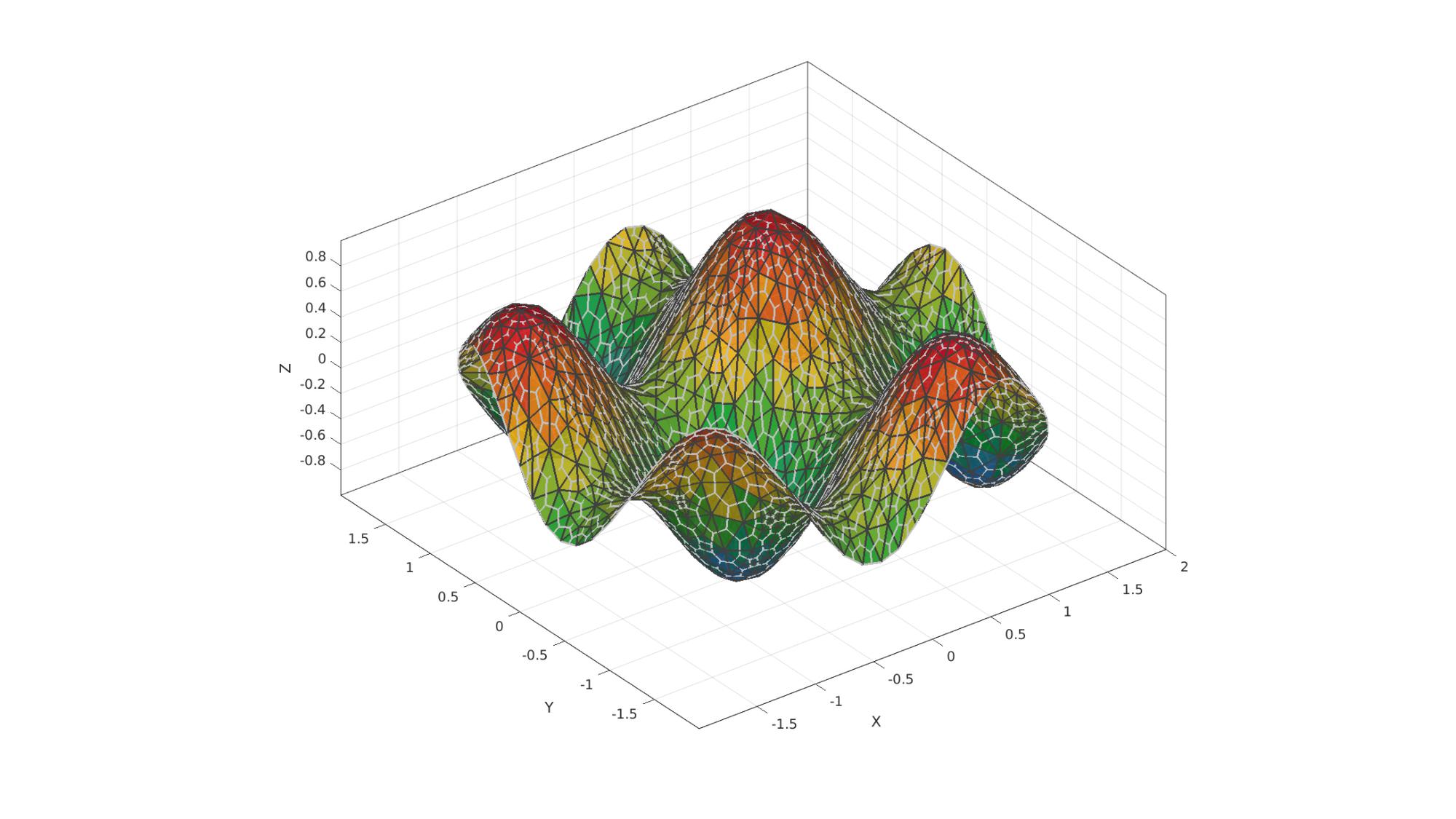
Example 1: Computing the dual of a surface triangulation

Creating example triangulation (circle filled triangle)

%Boundary and mesh parameters
ns=50; %Number of points on outer boundary (defines how well the circle is sampled)
rOut=2; %Outer radius of circular boundary
pointSpacing=rOut/15; %Approximate initial point spacing for point seeding
stdP=pointSpacing/2*ones(1,2); %Standard deviations for random point offset after point seeding

%Creating boundary curve
tt=linspace(0,2*pi,ns);
tt=tt(1:end-1);
r=rOut.*ones(size(tt));
[x,y] = pol2cart(tt,r);
Vb=[x(:) y(:)];

%Create Delaunay derived mesh
regionCell={Vb};
[F,V,~,DT]=regionTriMeshRand2D(regionCell,pointSpacing,stdP,1,0);
V(:,3)=(sin(3*V(:,1))+sin(3*V(:,2)))/2;

%Deriving the dual of the patch
[Vd,Fd]=patch_dual(V,F);

%Plotting results

cFigure; hold on;
gpatch(F,V,V(:,3),plotColor1,0.9,edgeWidth);
gpatch(Fd,Vd,'none',plotColor2,1,edgeWidth);
axisGeom(gca,fontSize);
camlight headlight;
colormap(cMap);
drawnow;

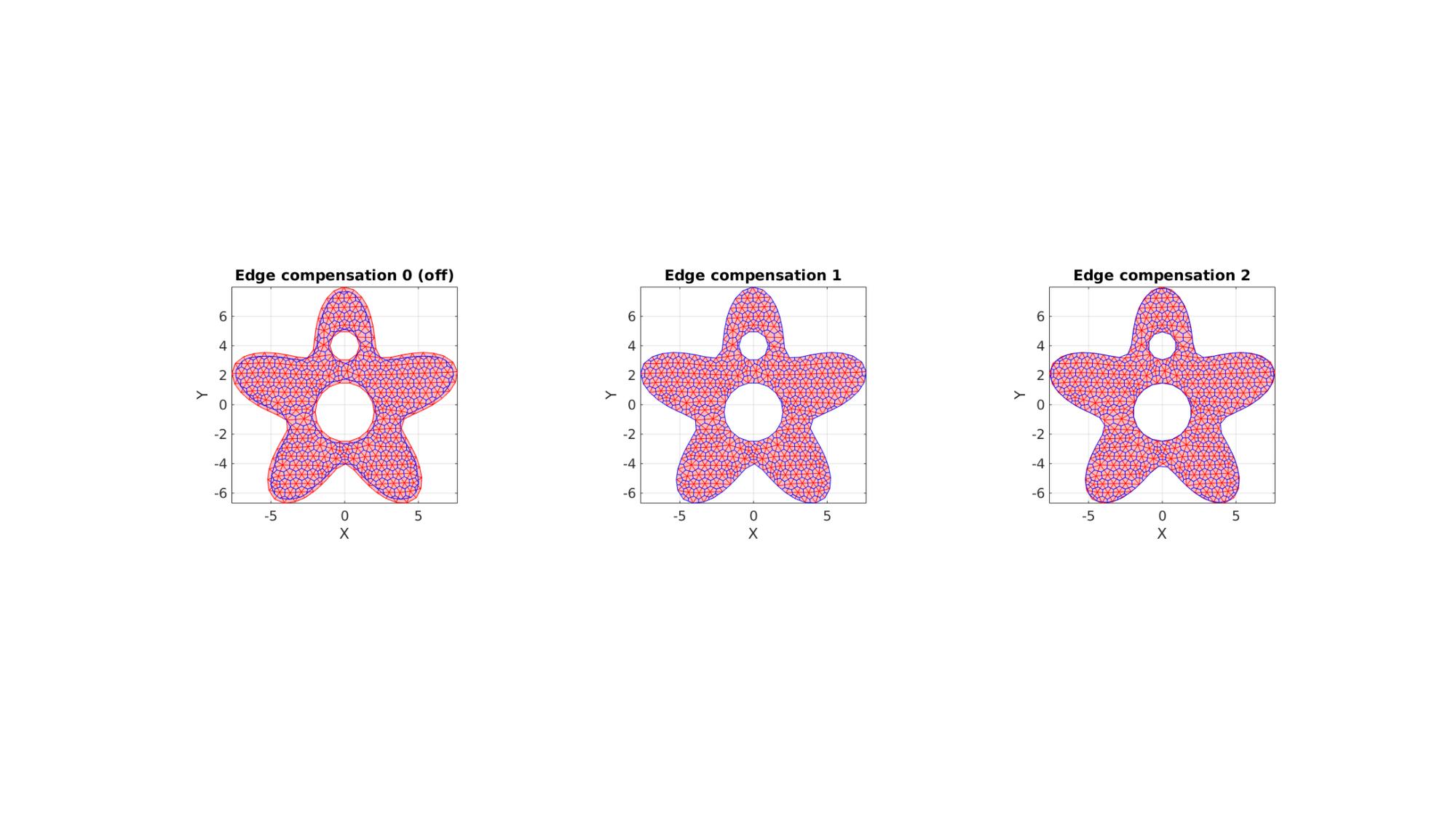
Example 2: Methods for handling the boundary

%Boundary 1
ns=150;
t=linspace(0,2*pi,ns);
t=t(1:end-1);
r=6+2.*sin(5*t);
[x,y] = pol2cart(t,r);
V1=[x(:) y(:)];

%Boundary 2
[x,y] = pol2cart(t,ones(size(t)));
V2=[x(:) y(:)+4];

%Boundary 3
[x,y] = pol2cart(t,2*ones(size(t)));
V3=[x(:) y(:)-0.5];

%Meshing the region
pointSpacing=0.75; %Desired point spacing
[F,V]=regionTriMesh2D({V1,V2,V3},pointSpacing,1,0);

Deriving the dual of the patch while treating boundary using three different methods.

fixBoundaryOption=0;
[Vd0,Fd0]=patch_dual(V,F,fixBoundaryOption);

fixBoundaryOption=1;
[Vd1,Fd1]=patch_dual(V,F,fixBoundaryOption);

fixBoundaryOption=2;
[Vd2,Fd2]=patch_dual(V,F,fixBoundaryOption);

%Plotting results

cFigure;
subplot(1,3,1); hold on;
title('Edge compensation 0 (off)');
gpatch(F,V,'rw','r',0.5);
gpatch(Fd0,Vd0,'none','b',1);
axisGeom(gca,fontSize);
colormap(cMap);
view(2);

subplot(1,3,2); hold on;
title('Edge compensation 1');
gpatch(F,V,'rw','r',0.5);
gpatch(Fd1,Vd1,'none','b',1);
axisGeom(gca,fontSize);
view(2);

subplot(1,3,3); hold on;
title('Edge compensation 2');
gpatch(F,V,'rw','r',0.5);
gpatch(Fd2,Vd2,'none','b',1);
axisGeom(gca,fontSize);
view(2);

drawnow;

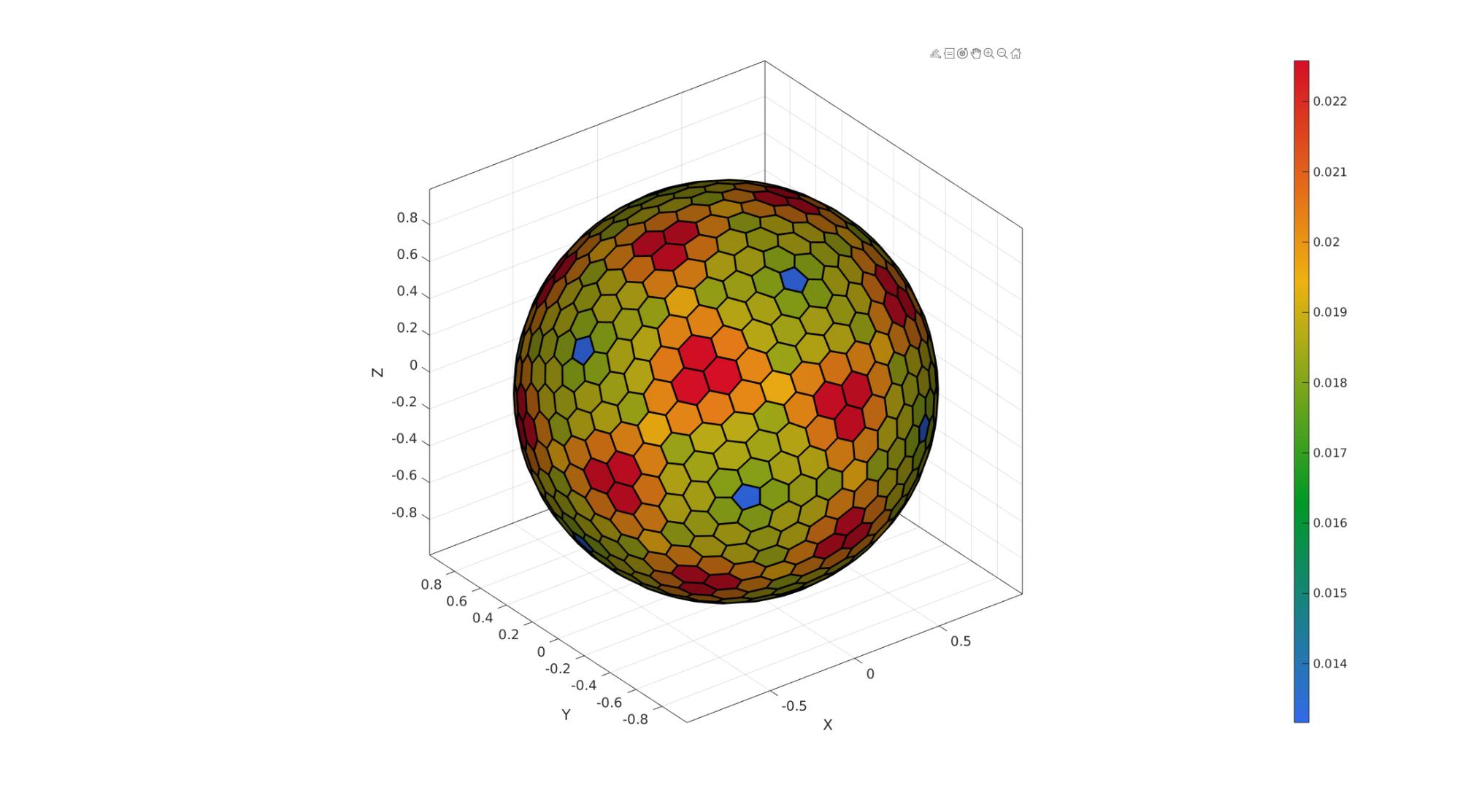
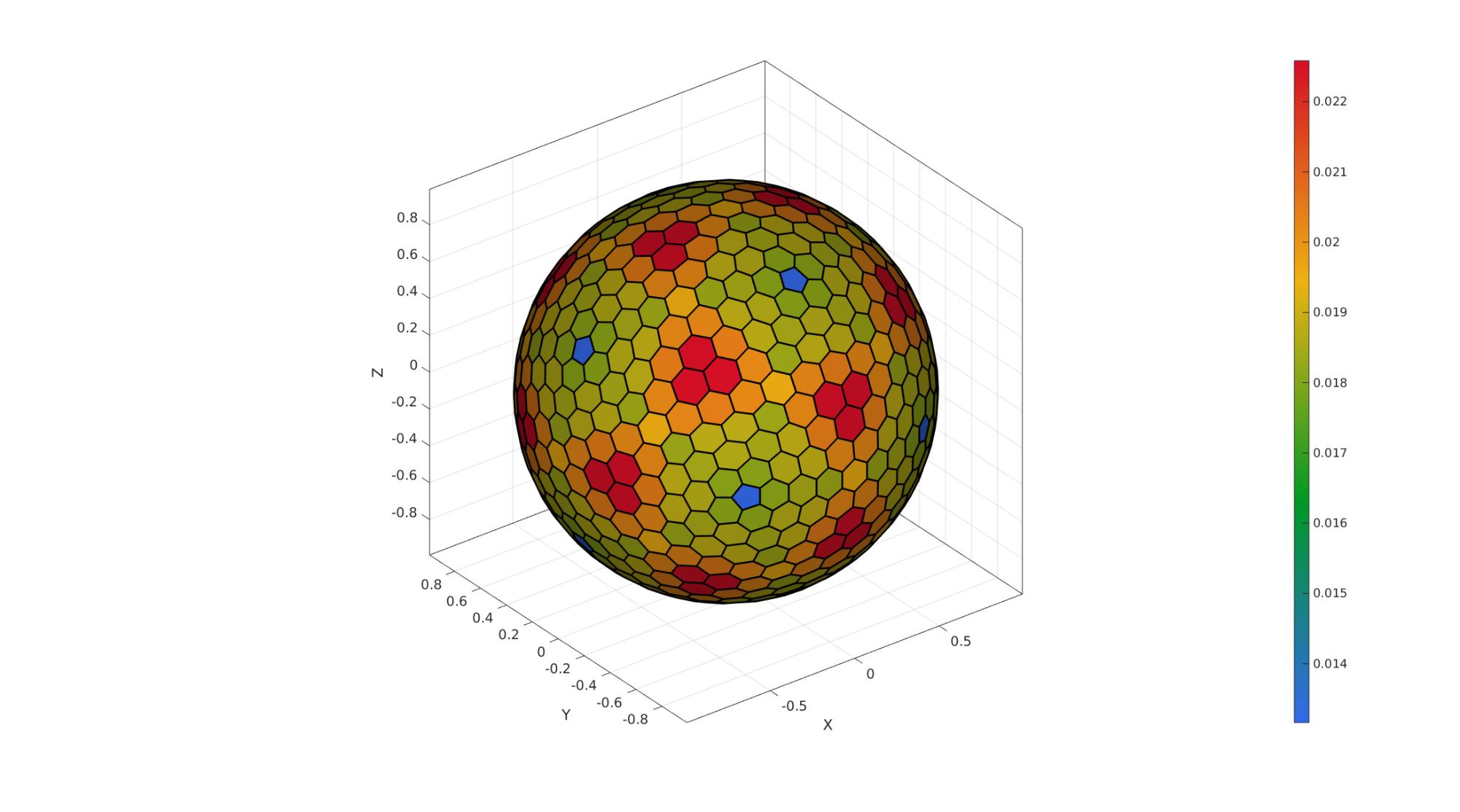
Example 3: The "Buckminster Fuller" dome triangulation and its dual

The patch_dual function assumes that a valid and appropriate dual exists for the input patch data specified by F and V (faces and vertices). If they are not appropriate the output may for instance not form an enclosing shape or output faces may not be planar.

%Defining geodesic dome triangulation
r=1; %sphere radius
n=3; %Refinements
[F,V,~]=geoSphere(n,r);

%Deriving the dual of the patch
[Vd,Fd]=patch_dual(V,F);

Ad=patchArea(Fd,Vd);

%Plotting results

cFigure; hold on;
% gpatch(F,V,'none','w',1,0.5);
% plotV(V,'k.','MarkerSize',markerSize);
gpatch(Fd,Vd,Ad,'k',1,edgeWidth);
% plotV(Vd,'k.','MarkerSize',markerSize);
axisGeom(gca,fontSize);
axisGeom(gca,fontSize); camlight headlight;
colormap(cMap); colorbar;
drawnow;

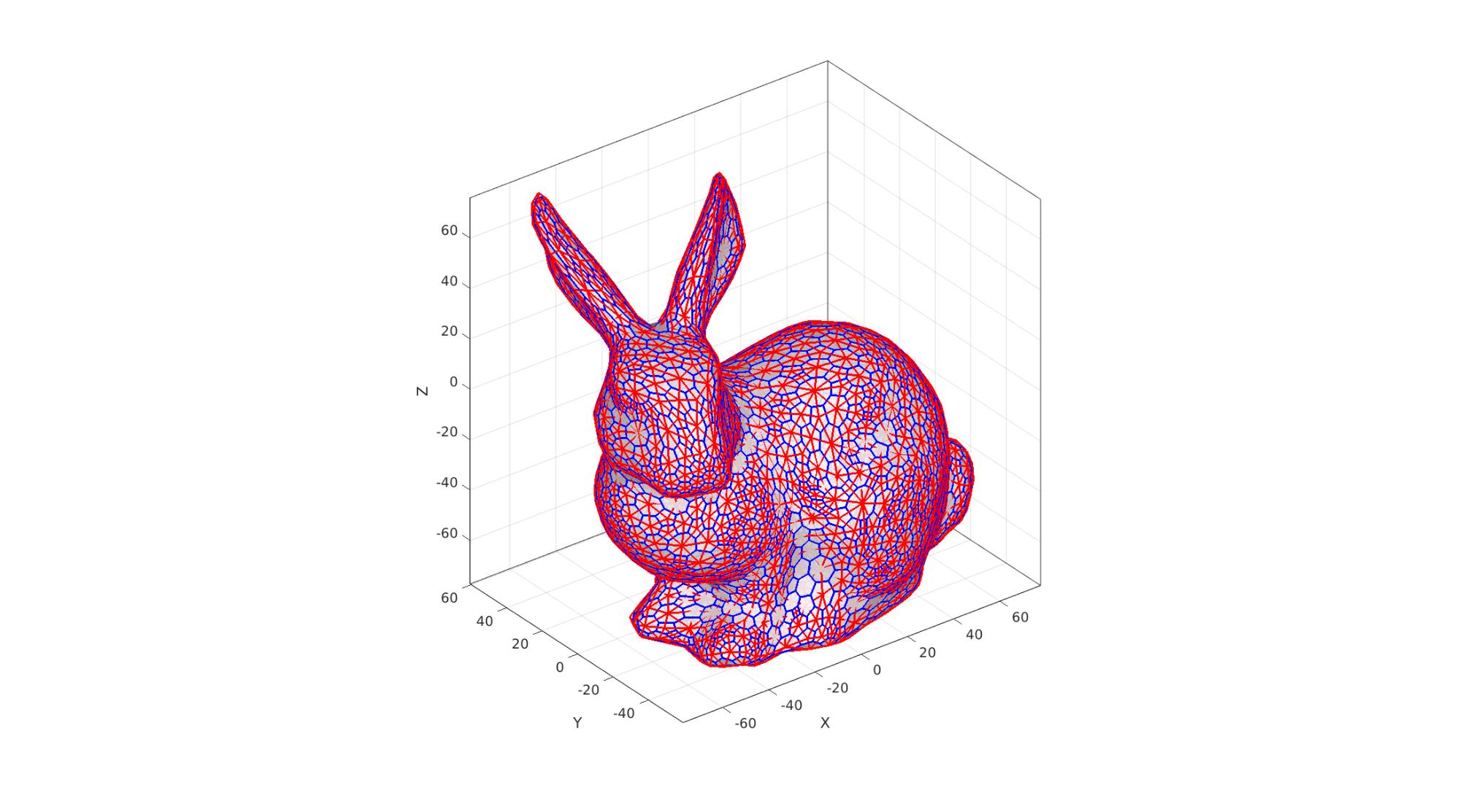
Example 4: Bunny

%Defining geodesic dome triangulation
[F,V]=stanford_bunny;

%Deriving the dual of the patch
[Vd,Fd]=patch_dual(V,F);

%Plotting results

cFigure; hold on;
gpatch(F,V,'none','r',1,edgeWidth);
gpatch(Fd,Vd,'w','b',0.9,edgeWidth);
% patchNormPlot(Fd,Vd);
axisGeom(gca,fontSize);
camlight headlight;

drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2006-2023 Kevin Mattheus Moerman and the GIBBON contributors

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2023a