patchcylinder

Below is a demonstration of the features of the patchcylinder function

Syntax
Description
Examples
Building a patched cylinder model
Using an input structure instead
Creating a closed cylinder model

Syntax

[F,V]=patchcylinder(r,nr,h,nz,ptype);

Description

Use patchcylinder to generate triangulated spheres with nearly geodesic triangle distributions. The density of the triangulation can be controlled through a particular choice of n (number of mesh refinement steps).

Examples

clear; close all; clc;

Plot Settings

fontSize=15;
faceAlpha=0.8;
edgeColor=0.*ones(1,3);
edgeWidth=2;

Building a patched cylinder model

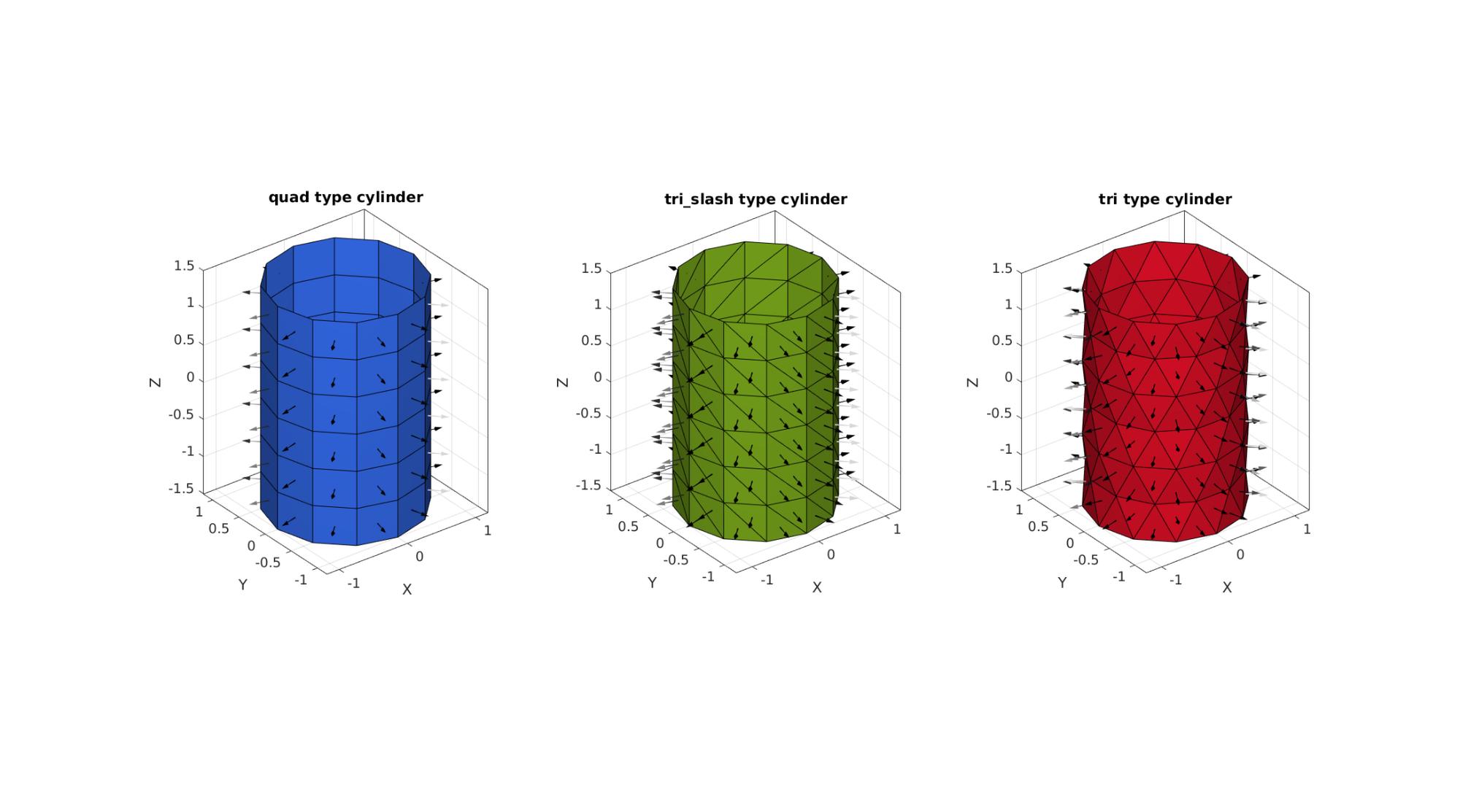
Defining patched cylinders with different mesh types

cylRaduis=1; %Cylinder radius
numRadial=12; %Number of elements in the circumferential direction
cylHeight=3; %height
numSteps=7; %Number of elements in the height direction
meshTypes={'quad','tri_slash','tri'}; %Patch Types

pColors=gjet(numel(meshTypes));

Creating and visualizing patch data

cFigure;
for q=1:1:numel(meshTypes)
    [F,V]=patchcylinder(cylRaduis,numRadial,cylHeight,numSteps,meshTypes{q});
    subplot(1,3,q); hold on;
    title([meshTypes{q},' type cylinder'],'FontSize',fontSize,'Interpreter','none');
    axisGeom(gca,fontSize);
    gpatch(F,V,pColors(q,:));
    patchNormPlot(F,V);
    camlight headlight;
end
drawnow;

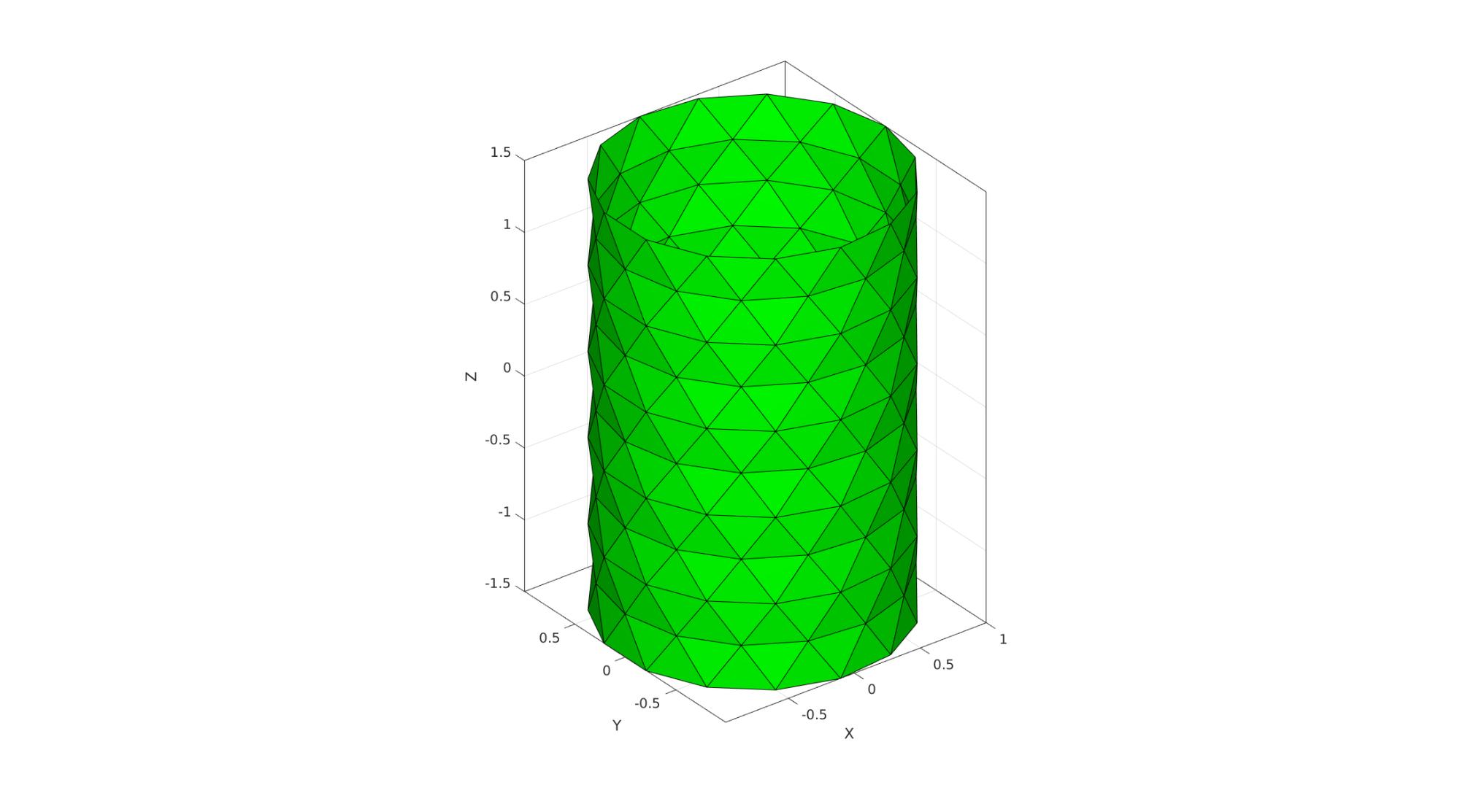
Using an input structure instead

Creating input structure

inputStruct.cylRadius=1;
inputStruct.numRadial=15;
inputStruct.cylHeight=3;
inputStruct.numHeight=11;
inputStruct.meshType='tri';

Derive patch data for a cylinder

[F,V]=patchcylinder(inputStruct);

Visualizing cylinder model

cFigure;
hold on;
gpatch(F,V,'g');
% patchNormPlot(F,V);
axisGeom(gca,fontSize);
camlight headlight;
drawnow;

Creating a closed cylinder model

% Creating input structure
inputStruct.cylRadius=1;
inputStruct.numRadial=15;
inputStruct.cylHeight=3;
inputStruct.numHeight=[]; %if empty infer from point spacing of circle
inputStruct.meshType='tri';
inputStruct.closeOpt=1;

Derive patch data for a cylinder

[F,V,C]=patchcylinder(inputStruct);

Visualizing meshed regions

cFigure;
gpatch(F,V,C);
patchNormPlot(F,V);
colormap(gjet(3)); icolorbar;
axisGeom;
camlight headlight;
drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.