polyRevolve

Below is a demonstration of the features of the polyRevolve function

Contents

Syntax

[F_tri,V_tri]=polyRevolve(Vc,cPar);

Description

The polyRevolve function can be used to revolve polygons to obtain surface patch data and generate CAD like model geometry. See also: polyExtrude and polyLoftLinear

Examples

clear; close all; clc;

Plot settings

fontSize=15;
lineWidth=8;

Example: Revolving a polygon

Creating an example polygon (or sketch)

ns=15;
x=linspace(0,2*pi,ns)+1;
y=zeros(size(x));
z=-cos(x);

Vc=[x(:) y(:) z(:)];

Revolving the polygon to obtain a surface model

cPar.closeLoopOpt=1;
cPar.numSteps=[]; %If empty the number of steps is derived from point spacing of input curve
cPar.w=[0 0 1];
[F,V,C]=polyRevolve(Vc,cPar);

Plotting results

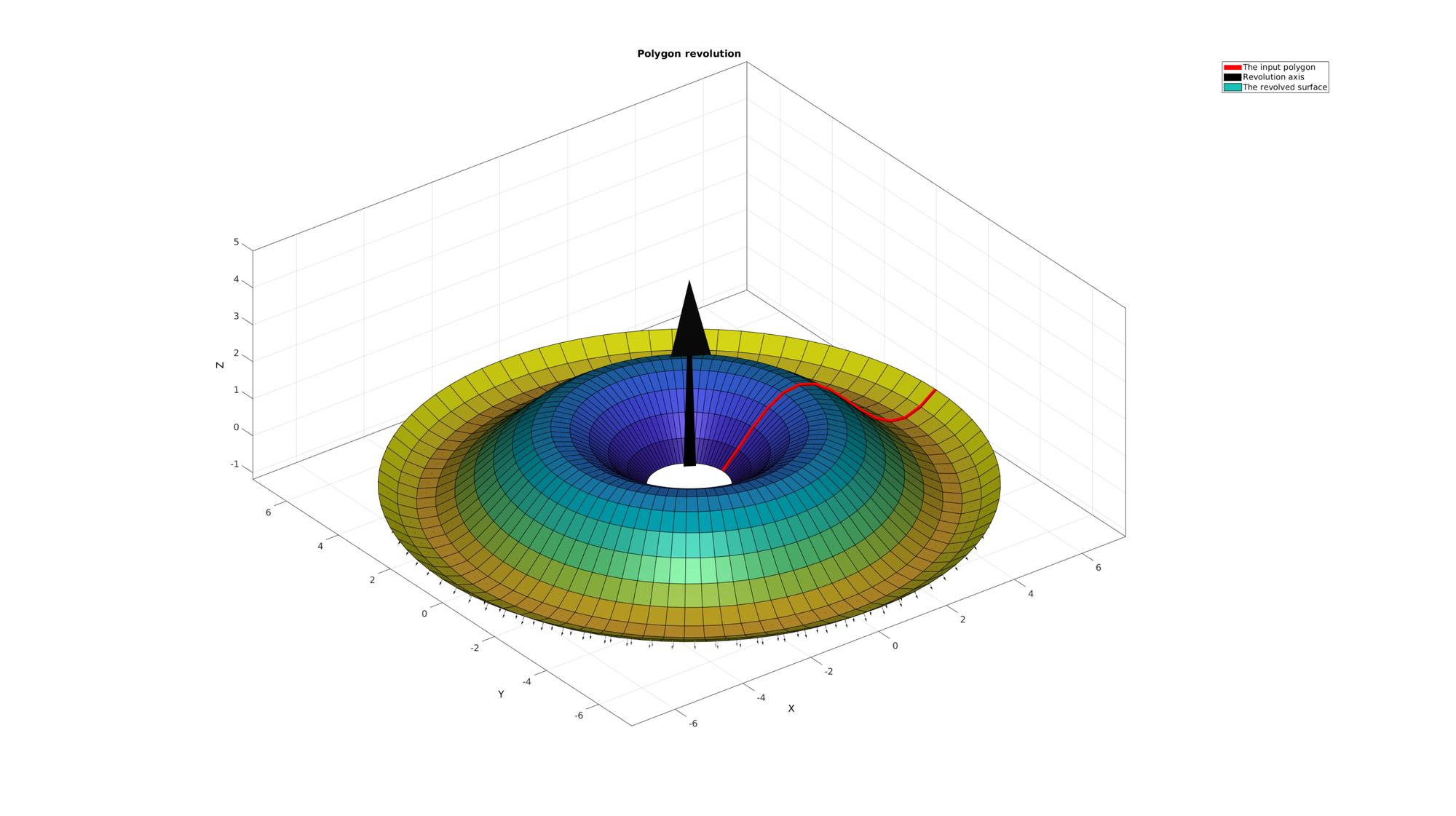
cFigure;
title('Polygon revolution','FontSize',fontSize);
hold on;

hp1=plotV(Vc,'r-','lineWidth',lineWidth);
hp2=quiverVec([0 0 0],cPar.w,5,'k');
hp3=gpatch(F,V,C,'k');
patchNormPlot(F,V);
axisGeom(gca,fontSize);
camlight headlight;
legend([hp1 hp2 hp3],'The input polygon','Revolution axis','The revolved surface');
drawnow;

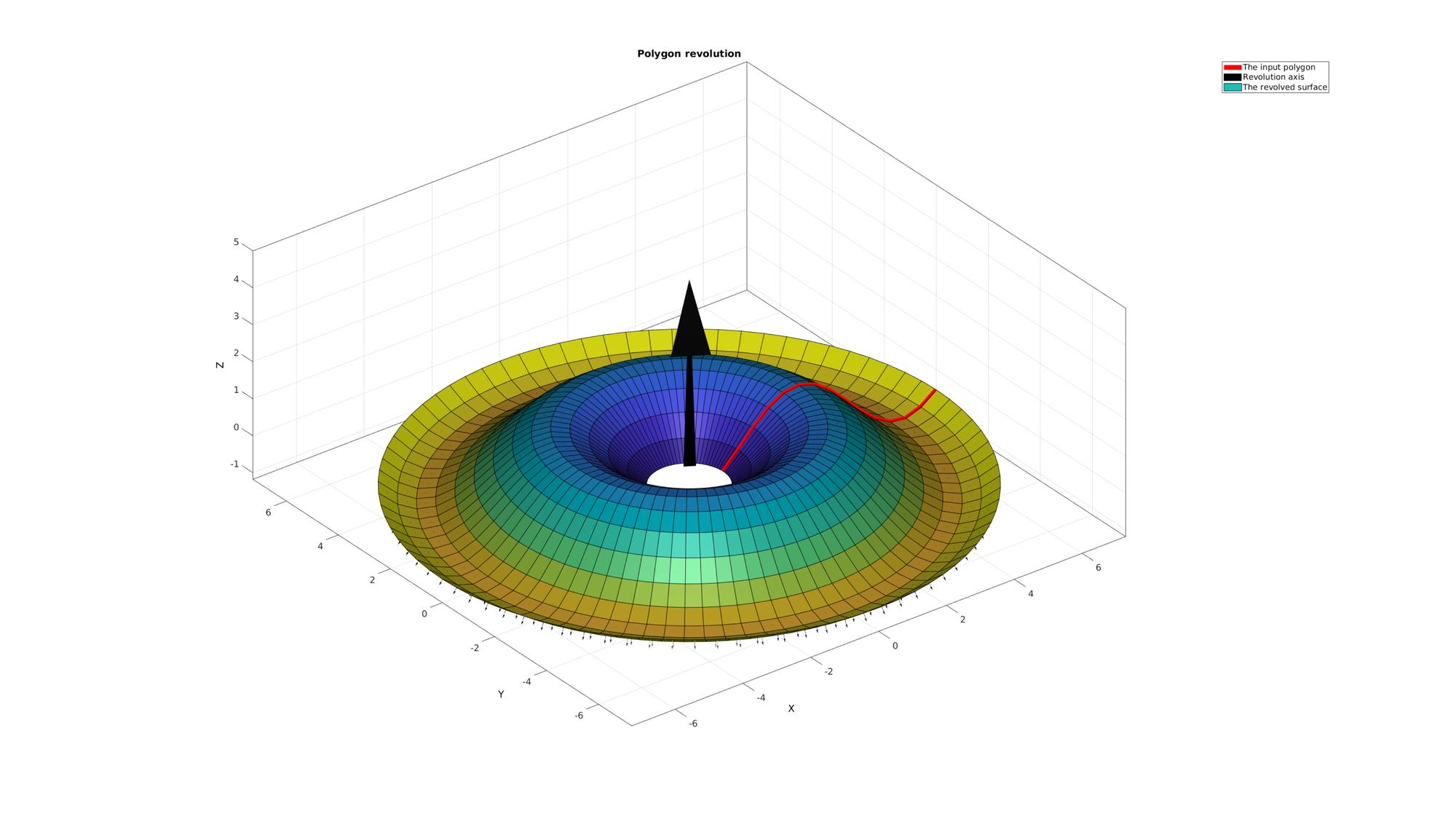
Example: Revolving a closed polygon

Creating an example polygon (or sketch)

ns=15;
t=linspace(0,2*pi,ns);
r=1;
x=r*sin(t)+3*r;
y=zeros(size(x));
z=r*cos(t);

Vc=[x(:) y(:) z(:)];

Revolving the polygon to obtain a surface model

cPar.closeLoopOpt=1;
cPar.numSteps=[]; %If empty the number of steps is derived from point spacing of input curve
cPar.w=[0 0 1]; %Revolution axis
cPar.theta=1*pi; %revolution angle
cPar.closeLoopOpt=0; %Do not close by attaching ends
[F,V,C]=polyRevolve(Vc,cPar);

Plotting results

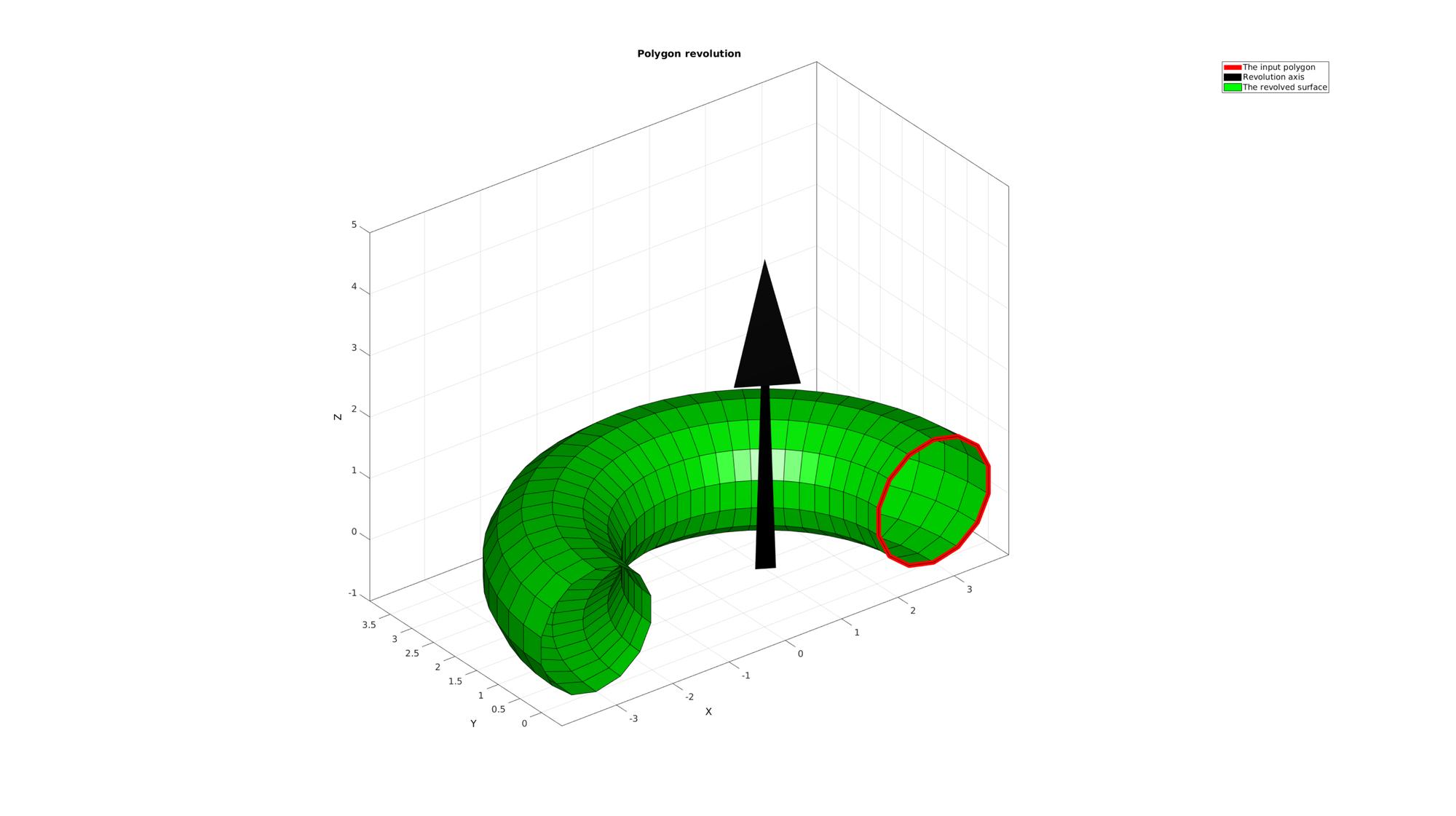
cFigure;
title('Polygon revolution','FontSize',fontSize);
hold on;

hp1=plotV(Vc,'r-','lineWidth',lineWidth);
hp2=quiverVec([0 0 0],cPar.w,5,'k');
hp3=gpatch(F,V,'g','k');

axisGeom(gca,fontSize);
camlight headlight;
legend([hp1 hp2 hp3],'The input polygon','Revolution axis','The revolved surface');
drawnow;

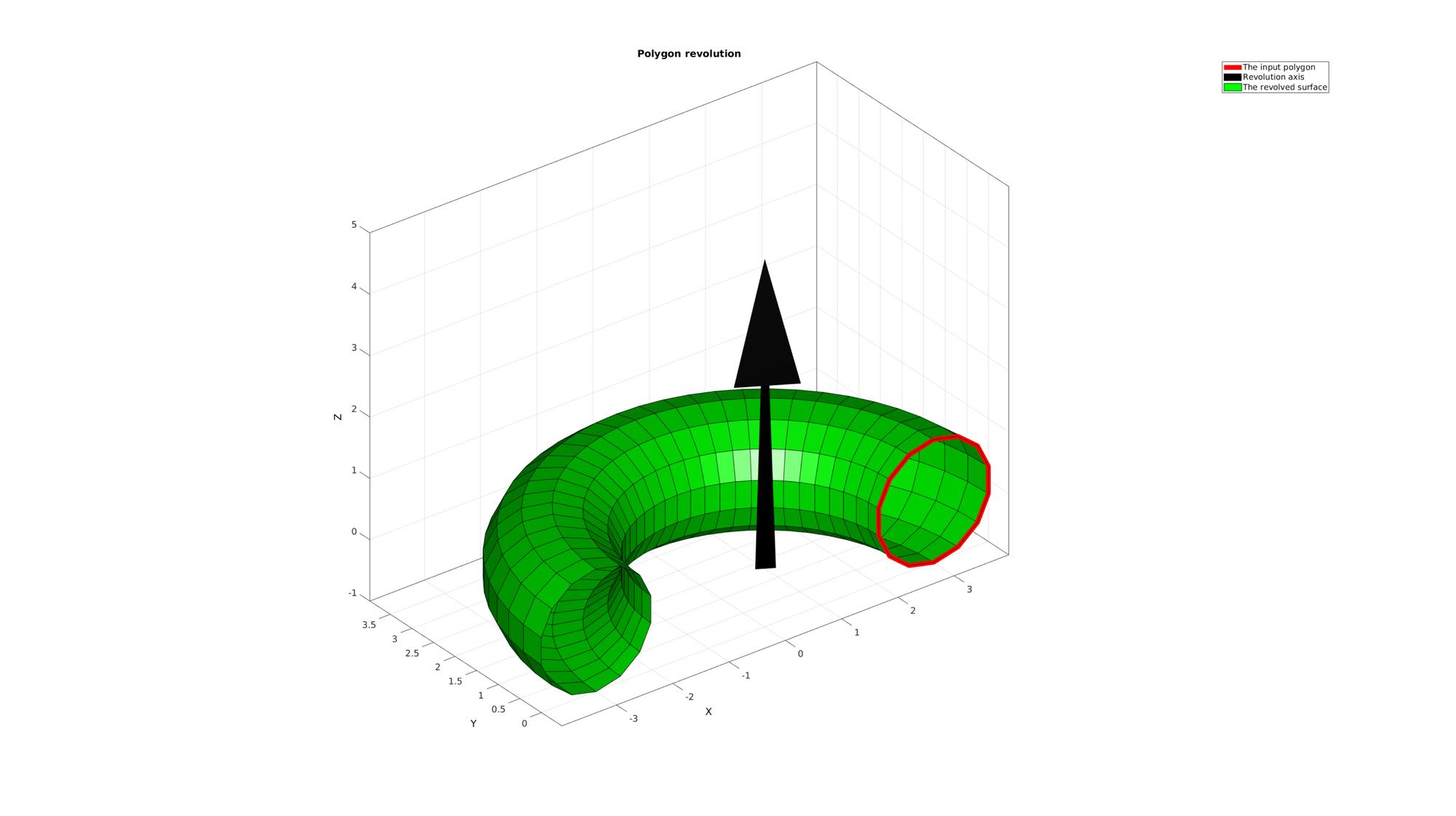
Example: Changing the axis of revolution

Creating an example polygon (or sketch)

ns=15;
x=linspace(0,6,ns)+1;
y=zeros(size(x));
z=x;

Vc=[x(:) y(:) z(:)];

Creating an example set of rotation axes

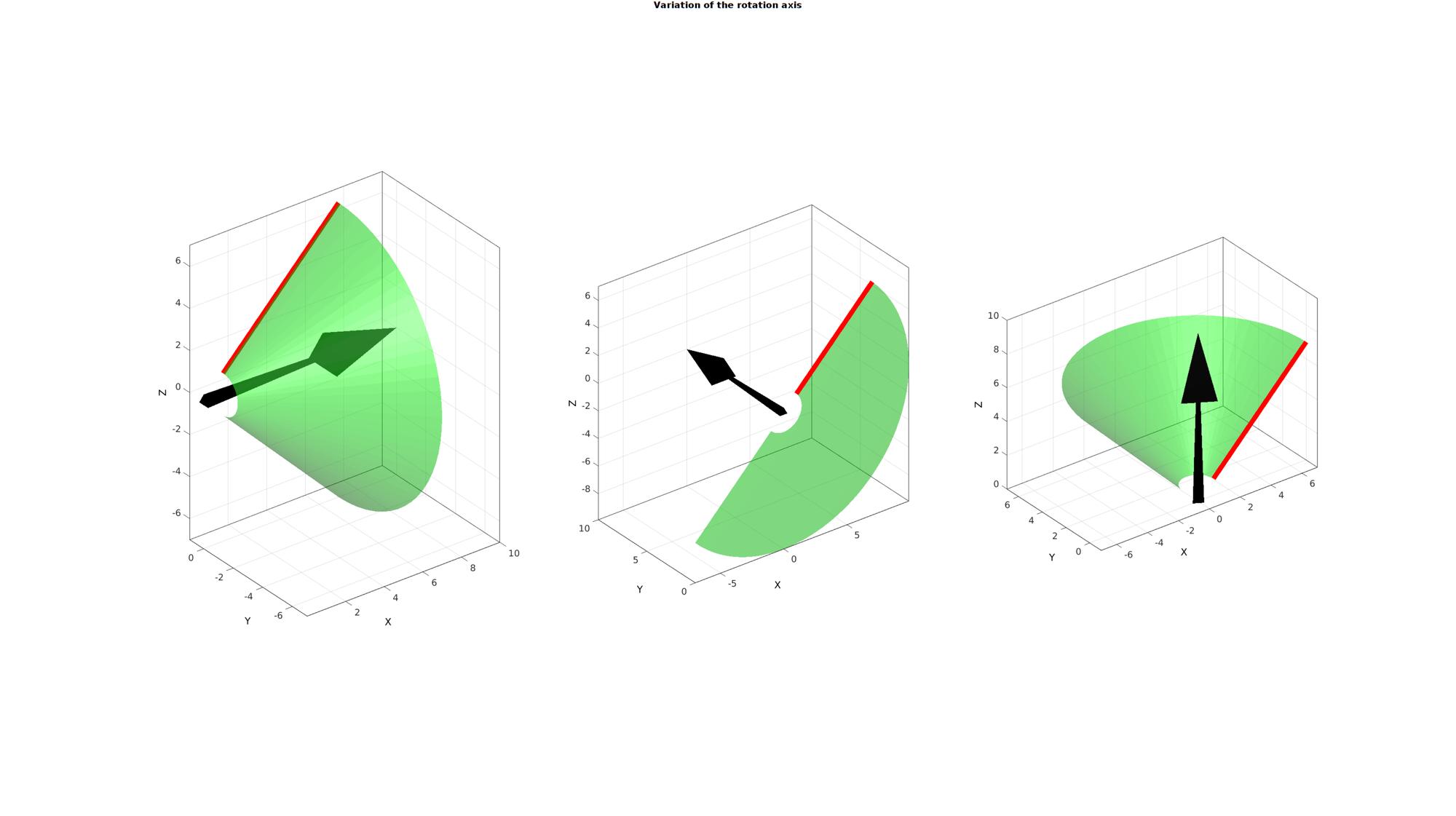
W=eye(3,3);

cFigure;
gtitle('Variation of the rotation axis',fontSize);
for q=1:1:size(W,1)

    cPar.w=W(q,:);
    [F,V,C]=polyRevolve(Vc,cPar);

    %Visualizing mesh
    subplot(1,size(W,1),q);
    % title(patchTypes{q},'FontSize',fontSize,'Interpreter','none');
    hold on;

    hp1=plotV(Vc,'r-','lineWidth',lineWidth);
    hp2=quiverVec([0 0 0],cPar.w,10,'k');
    hp3=gpatch(F,V,'g','none',0.5);

    axisGeom(gca,fontSize);
    camlight headlight;

end

drawnow;

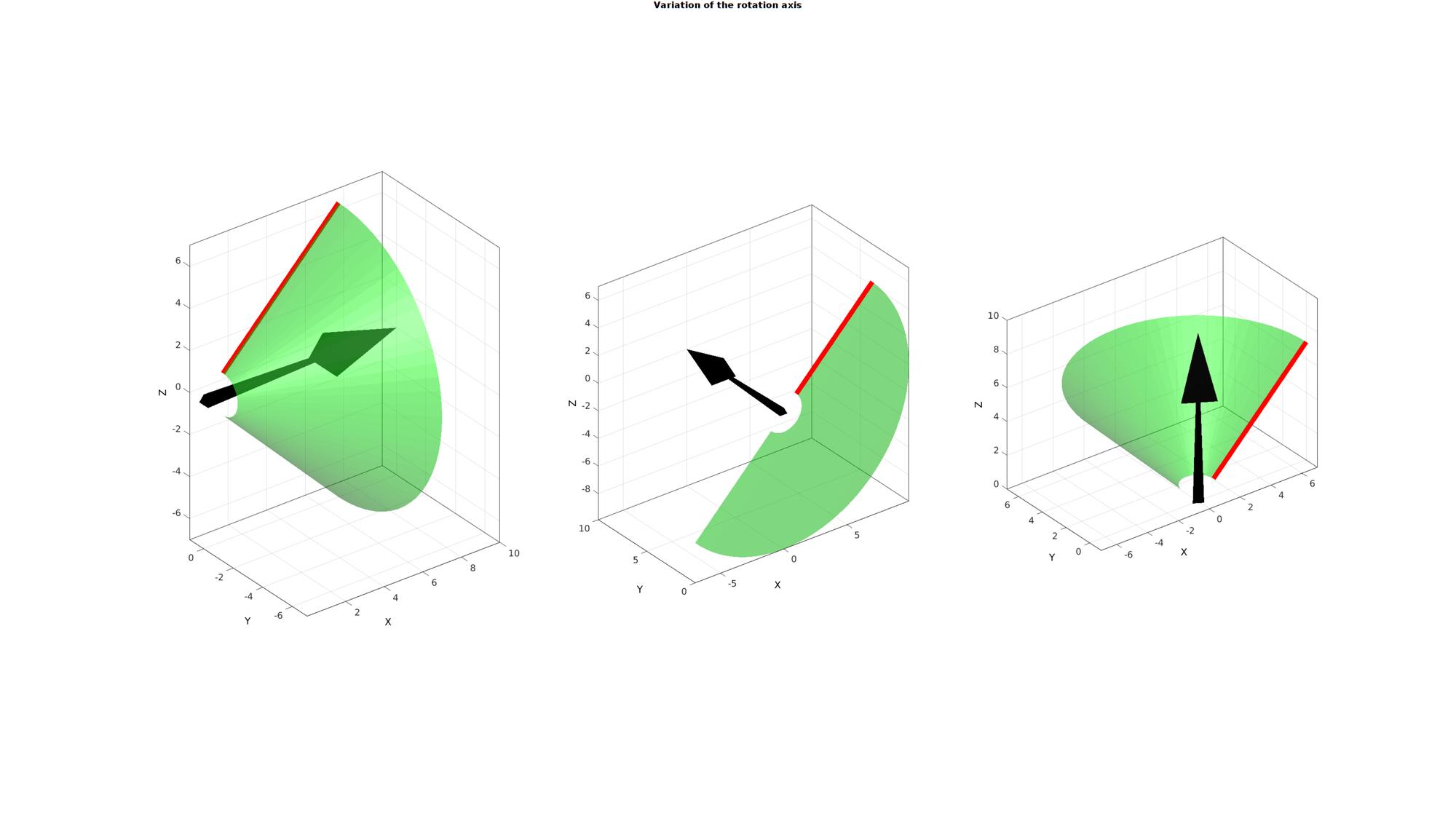
Example: Changing the angle of revolution

Creating an example polygon (or sketch)

ns=15;
x=linspace(0,2*pi,ns)+1;
y=zeros(size(x));
z=sin(x);

Vc=[x(:) y(:) z(:)];

Creating an example set of angles

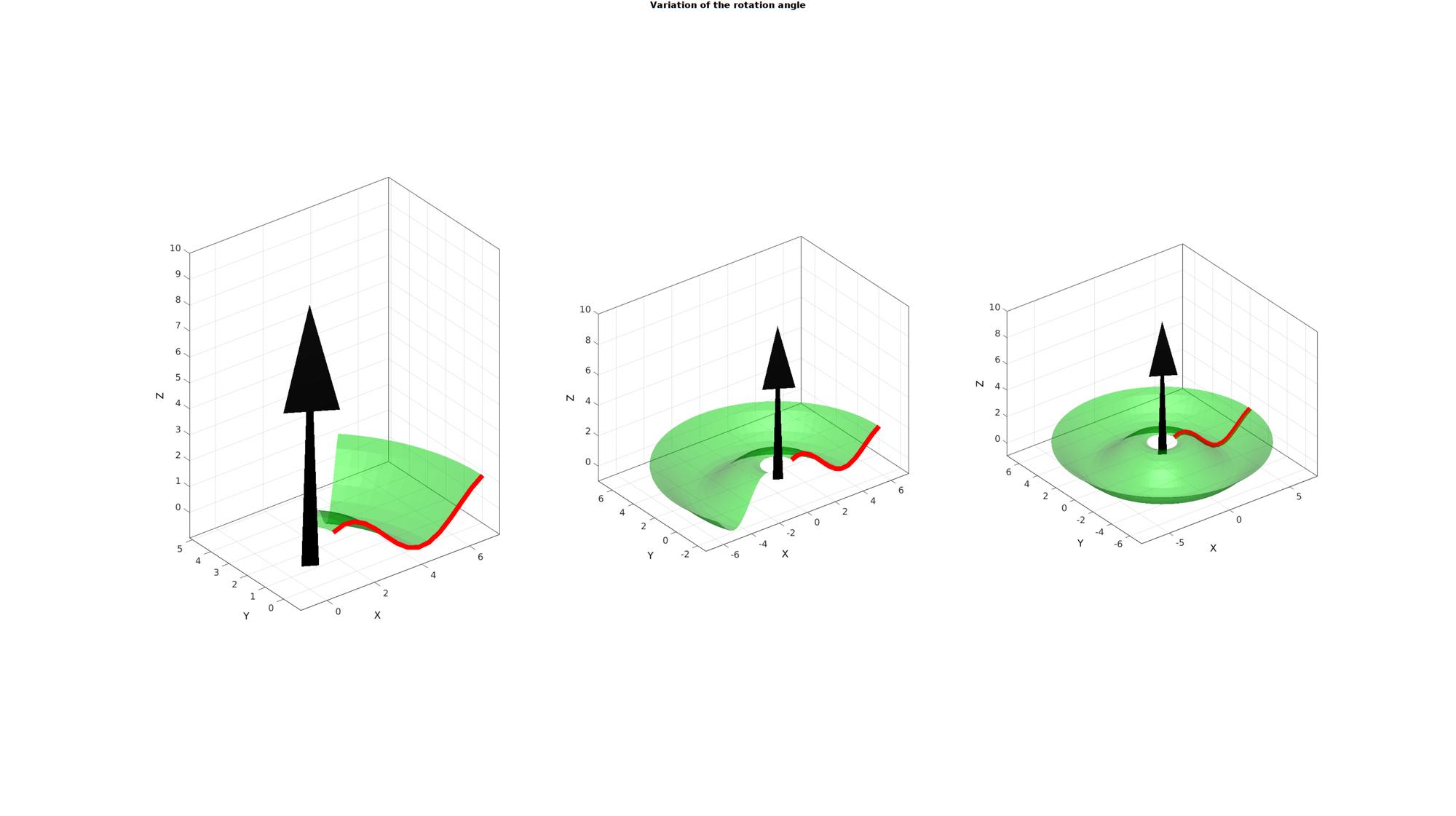
T=linspace(0.25*pi,2*pi,3);
cPar.w=[0 0 1];
cPar.closeLoopOpt=0; %Do not close feature

cFigure;
gtitle('Variation of the rotation angle',fontSize);
for q=1:1:size(W,1)

    cPar.theta=T(q);
    [F,V,C]=polyRevolve(Vc,cPar);

    %Visualizing mesh
    subplot(1,size(W,1),q);
    % title(patchTypes{q},'FontSize',fontSize,'Interpreter','none');
    hold on;

    hp1=plotV(Vc,'r-','lineWidth',lineWidth);
    hp2=quiverVec([0 0 0],cPar.w,10,'k');
    hp3=gpatch(F,V,'g','none',0.5);

    axisGeom(gca,fontSize);
    camlight headlight;

end

drawnow;

GIBBON www.gibboncode.org

Kevin Mattheus Moerman, [email protected]

GIBBON footer text

License: https://github.com/gibbonCode/GIBBON/blob/master/LICENSE

GIBBON: The Geometry and Image-based Bioengineering add-On. A toolbox for image segmentation, image-based modeling, meshing, and finite element analysis.

Copyright (C) 2019 Kevin Mattheus Moerman

This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Published with MATLAB® R2019a